Kinetic Interacting Particle Langevin Monte Carlo
Paper and Code
Jul 08, 2024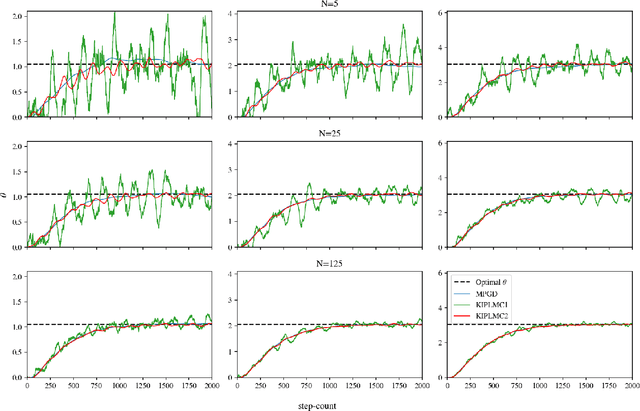

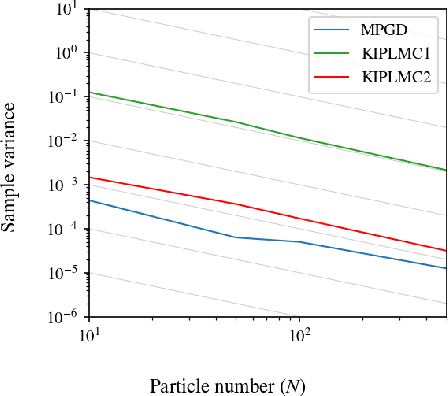
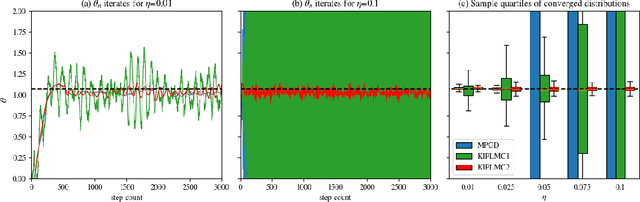
This paper introduces and analyses interacting underdamped Langevin algorithms, termed Kinetic Interacting Particle Langevin Monte Carlo (KIPLMC) methods, for statistical inference in latent variable models. We propose a diffusion process that evolves jointly in the space of parameters and latent variables and exploit the fact that the stationary distribution of this diffusion concentrates around the maximum marginal likelihood estimate of the parameters. We then provide two explicit discretisations of this diffusion as practical algorithms to estimate parameters of statistical models. For each algorithm, we obtain nonasymptotic rates of convergence for the case where the joint log-likelihood is strongly concave with respect to latent variables and parameters. In particular, we provide convergence analysis for the diffusion together with the discretisation error, providing convergence rate estimates for the algorithms in Wasserstein-2 distance. To demonstrate the utility of the introduced methodology, we provide numerical experiments that demonstrate the effectiveness of the proposed diffusion for statistical inference and the stability of the numerical integrators utilised for discretisation. Our setting covers a broad number of applications, including unsupervised learning, statistical inference, and inverse problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge