On the contraction properties of Sinkhorn semigroups

We develop a novel semigroup contraction analysis based on Lyapunov techniques to prove the exponential convergence of Sinkhorn equations on weighted Banach spaces. This operator-theoretic framework yields exponential decays of Sinkhorn iterates towards Schr\"odinger bridges with respect to general classes of $\phi$-divergences as well as in weighted Banach spaces. To the best of our knowledge, these are the first results of this type in the literature on entropic transport and the Sinkhorn algorithm. We also illustrate the impact of these results in the context of multivariate linear Gaussian models as well as statistical finite mixture models including Gaussian-kernel density estimation of complex data distributions arising in generative models.

The Incremental Proximal Method: A Probabilistic Perspective

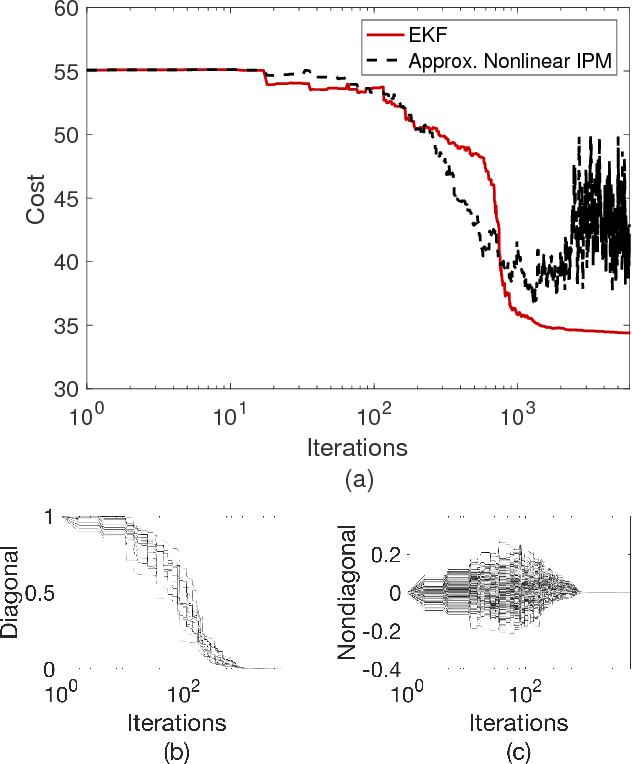
In this work, we highlight a connection between the incremental proximal method and stochastic filters. We begin by showing that the proximal operators coincide, and hence can be realized with, Bayes updates. We give the explicit form of the updates for the linear regression problem and show that there is a one-to-one correspondence between the proximal operator of the least-squares regression and the Bayes update when the prior and the likelihood are Gaussian. We then carry out this observation to a general sequential setting: We consider the incremental proximal method, which is an algorithm for large-scale optimization, and show that, for a linear-quadratic cost function, it can naturally be realized by the Kalman filter. We then discuss the implications of this idea for nonlinear optimization problems where proximal operators are in general not realizable. In such settings, we argue that the extended Kalman filter can provide a systematic way for the derivation of practical procedures.