Learning state and proposal dynamics in state-space models using differentiable particle filters and neural networks

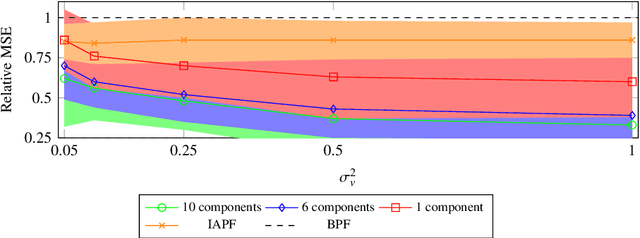
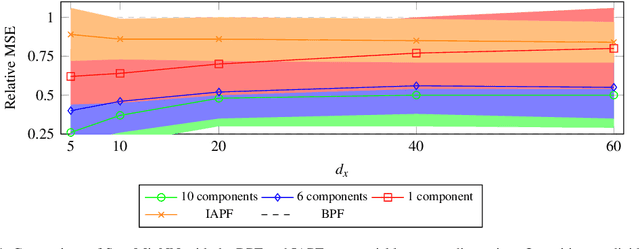
State-space models are a popular statistical framework for analysing sequential data. Within this framework, particle filters are often used to perform inference on non-linear state-space models. We introduce a new method, StateMixNN, that uses a pair of neural networks to learn the proposal distribution and transition distribution of a particle filter. Both distributions are approximated using multivariate Gaussian mixtures. The component means and covariances of these mixtures are learnt as outputs of learned functions. Our method is trained targeting the log-likelihood, thereby requiring only the observation series, and combines the interpretability of state-space models with the flexibility and approximation power of artificial neural networks. The proposed method significantly improves recovery of the hidden state in comparison with the state-of-the-art, showing greater improvement in highly non-linear scenarios.

Regime Learning for Differentiable Particle Filters

Differentiable particle filters are an emerging class of models that combine sequential Monte Carlo techniques with the flexibility of neural networks to perform state space inference. This paper concerns the case where the system may switch between a finite set of state-space models, i.e. regimes. No prior approaches effectively learn both the individual regimes and the switching process simultaneously. In this paper, we propose the neural network based regime learning differentiable particle filter (RLPF) to address this problem. We further design a training procedure for the RLPF and other related algorithms. We demonstrate competitive performance compared to the previous state-of-the-art algorithms on a pair of numerical experiments.

Deep State-Space Model for Predicting Cryptocurrency Price

Our work presents two fundamental contributions. On the application side, we tackle the challenging problem of predicting day-ahead crypto-currency prices. On the methodological side, a new dynamical modeling approach is proposed. Our approach keeps the probabilistic formulation of the state-space model, which provides uncertainty quantification on the estimates, and the function approximation ability of deep neural networks. We call the proposed approach the deep state-space model. The experiments are carried out on established cryptocurrencies (obtained from Yahoo Finance). The goal of the work has been to predict the price for the next day. Benchmarking has been done with both state-of-the-art and classical dynamical modeling techniques. Results show that the proposed approach yields the best overall results in terms of accuracy.

Sparse Graphical Linear Dynamical Systems

Time-series datasets are central in numerous fields of science and engineering, such as biomedicine, Earth observation, and network analysis. Extensive research exists on state-space models (SSMs), which are powerful mathematical tools that allow for probabilistic and interpretable learning on time series. Estimating the model parameters in SSMs is arguably one of the most complicated tasks, and the inclusion of prior knowledge is known to both ease the interpretation but also to complicate the inferential tasks. Very recent works have attempted to incorporate a graphical perspective on some of those model parameters, but they present notable limitations that this work addresses. More generally, existing graphical modeling tools are designed to incorporate either static information, focusing on statistical dependencies among independent random variables (e.g., graphical Lasso approach), or dynamic information, emphasizing causal relationships among time series samples (e.g., graphical Granger approaches). However, there are no joint approaches combining static and dynamic graphical modeling within the context of SSMs. This work proposes a novel approach to fill this gap by introducing a joint graphical modeling framework that bridges the static graphical Lasso model and a causal-based graphical approach for the linear-Gaussian SSM. We present DGLASSO (Dynamic Graphical Lasso), a new inference method within this framework that implements an efficient block alternating majorization-minimization algorithm. The algorithm's convergence is established by departing from modern tools from nonlinear analysis. Experimental validation on synthetic and real weather variability data showcases the effectiveness of the proposed model and inference algorithm.

Bayesian data fusion with shared priors

The integration of data and knowledge from several sources is known as data fusion. When data is available in a distributed fashion or when different sensors are used to infer a quantity of interest, data fusion becomes essential. In Bayesian settings, a priori information of the unknown quantities is available and, possibly, shared among the distributed estimators. When the local estimates are fused, such prior might be overused unless it is accounted for. This paper explores the effects of shared priors in Bayesian data fusion contexts, providing fusion rules and analysis to understand the performance of such fusion as a function of the number of collaborative agents and the uncertainty of the priors. Analytical results are corroborated through experiments in a variety of estimation and classification problems.

Efficient Bayes Inference in Neural Networks through Adaptive Importance Sampling

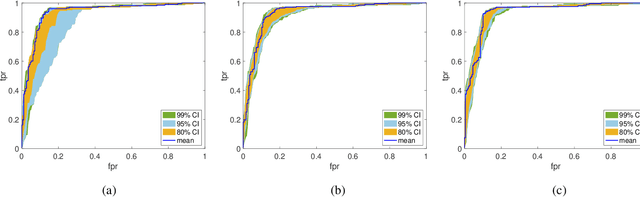
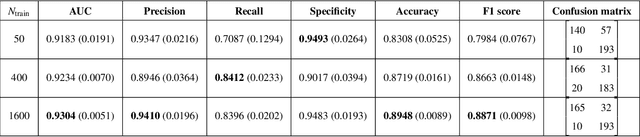
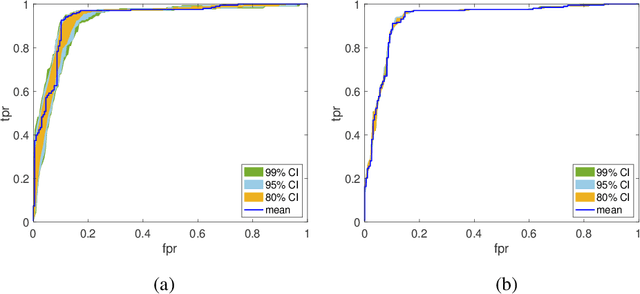
Bayesian neural networks (BNNs) have received an increased interest in the last years. In BNNs, a complete posterior distribution of the unknown weight and bias parameters of the network is produced during the training stage. This probabilistic estimation offers several advantages with respect to point-wise estimates, in particular, the ability to provide uncertainty quantification when predicting new data. This feature inherent to the Bayesian paradigm, is useful in countless machine learning applications. It is particularly appealing in areas where decision-making has a crucial impact, such as medical healthcare or autonomous driving. The main challenge of BNNs is the computational cost of the training procedure since Bayesian techniques often face a severe curse of dimensionality. Adaptive importance sampling (AIS) is one of the most prominent Monte Carlo methodologies benefiting from sounded convergence guarantees and ease for adaptation. This work aims to show that AIS constitutes a successful approach for designing BNNs. More precisely, we propose a novel algorithm PMCnet that includes an efficient adaptation mechanism, exploiting geometric information on the complex (often multimodal) posterior distribution. Numerical results illustrate the excellent performance and the improved exploration capabilities of the proposed method for both shallow and deep neural networks.

The Incremental Proximal Method: A Probabilistic Perspective

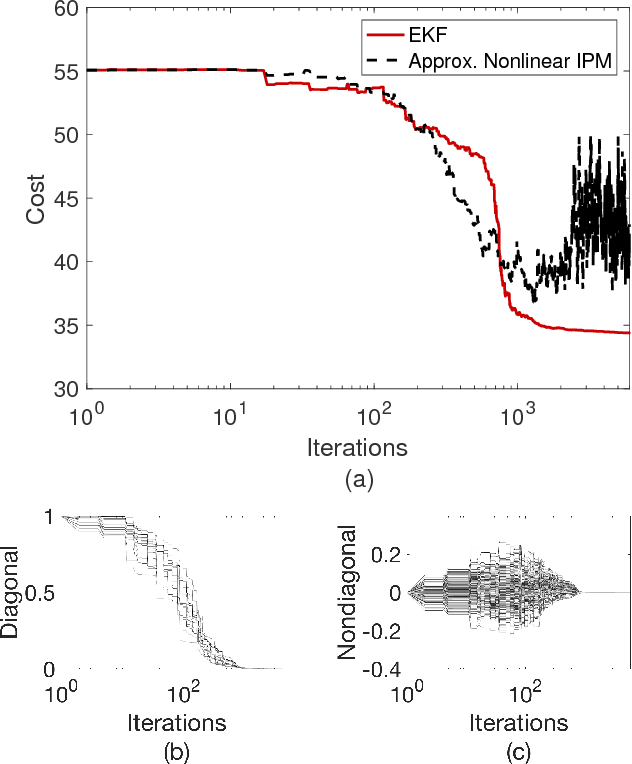
In this work, we highlight a connection between the incremental proximal method and stochastic filters. We begin by showing that the proximal operators coincide, and hence can be realized with, Bayes updates. We give the explicit form of the updates for the linear regression problem and show that there is a one-to-one correspondence between the proximal operator of the least-squares regression and the Bayes update when the prior and the likelihood are Gaussian. We then carry out this observation to a general sequential setting: We consider the incremental proximal method, which is an algorithm for large-scale optimization, and show that, for a linear-quadratic cost function, it can naturally be realized by the Kalman filter. We then discuss the implications of this idea for nonlinear optimization problems where proximal operators are in general not realizable. In such settings, we argue that the extended Kalman filter can provide a systematic way for the derivation of practical procedures.

Pattern Localization in Time Series through Signal-To-Model Alignment in Latent Space

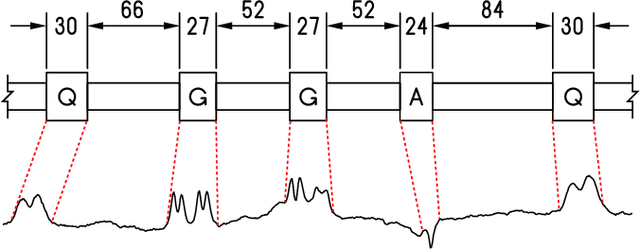
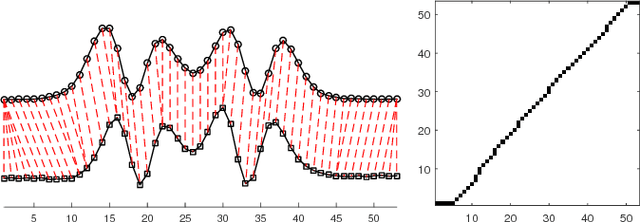
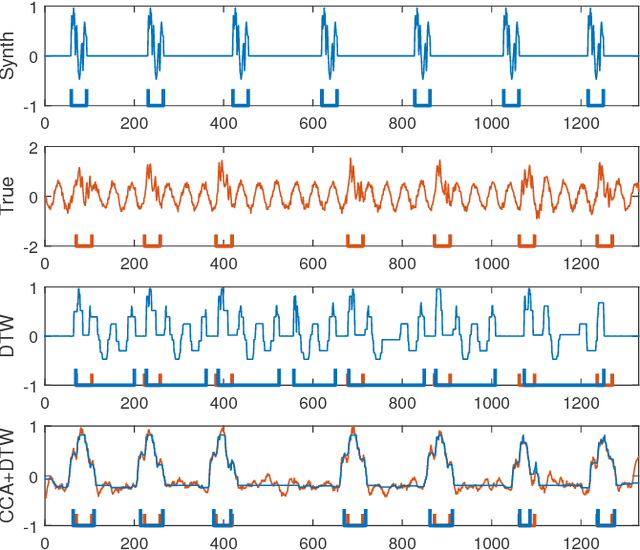
In this paper, we study the problem of locating a predefined sequence of patterns in a time series. In particular, the studied scenario assumes a theoretical model is available that contains the expected locations of the patterns. This problem is found in several contexts, and it is commonly solved by first synthesizing a time series from the model, and then aligning it to the true time series through dynamic time warping. We propose a technique that increases the similarity of both time series before aligning them, by mapping them into a latent correlation space. The mapping is learned from the data through a machine-learning setup. Experiments on data from non-destructive testing demonstrate that the proposed approach shows significant improvements over the state of the art.

The Recycling Gibbs Sampler for Efficient Learning

Monte Carlo methods are essential tools for Bayesian inference. Gibbs sampling is a well-known Markov chain Monte Carlo (MCMC) algorithm, extensively used in signal processing, machine learning, and statistics, employed to draw samples from complicated high-dimensional posterior distributions. The key point for the successful application of the Gibbs sampler is the ability to draw efficiently samples from the full-conditional probability density functions. Since in the general case this is not possible, in order to speed up the convergence of the chain, it is required to generate auxiliary samples whose information is eventually disregarded. In this work, we show that these auxiliary samples can be recycled within the Gibbs estimators, improving their efficiency with no extra cost. This novel scheme arises naturally after pointing out the relationship between the standard Gibbs sampler and the chain rule used for sampling purposes. Numerical simulations involving simple and real inference problems confirm the excellent performance of the proposed scheme in terms of accuracy and computational efficiency. In particular we give empirical evidence of performance in a toy example, inference of Gaussian processes hyperparameters, and learning dependence graphs through regression.