Differentiable Interacting Multiple Model Particle Filtering

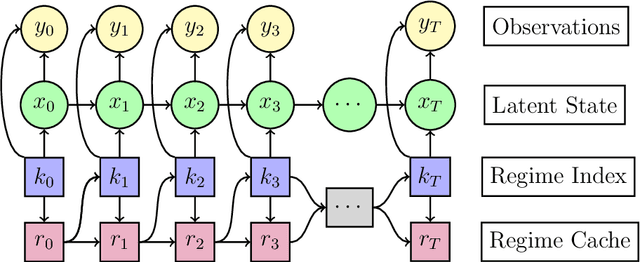
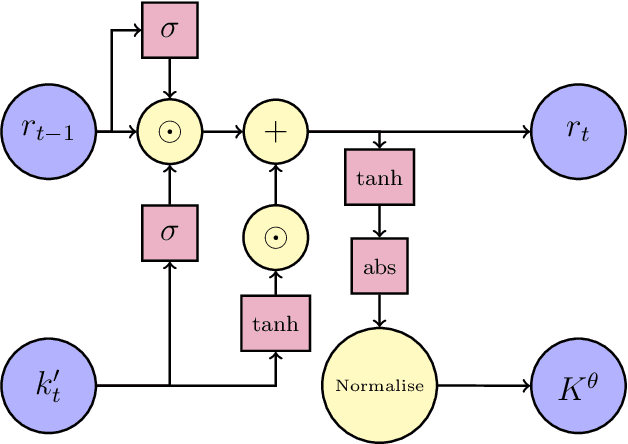
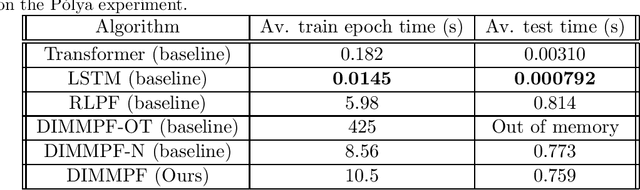
We propose a sequential Monte Carlo algorithm for parameter learning when the studied model exhibits random discontinuous jumps in behaviour. To facilitate the learning of high dimensional parameter sets, such as those associated to neural networks, we adopt the emerging framework of differentiable particle filtering, wherein parameters are trained by gradient descent. We design a new differentiable interacting multiple model particle filter to be capable of learning the individual behavioural regimes and the model which controls the jumping simultaneously. In contrast to previous approaches, our algorithm allows control of the computational effort assigned per regime whilst using the probability of being in a given regime to guide sampling. Furthermore, we develop a new gradient estimator that has a lower variance than established approaches and remains fast to compute, for which we prove consistency. We establish new theoretical results of the presented algorithms and demonstrate superior numerical performance compared to the previous state-of-the-art algorithms.

Regime Learning for Differentiable Particle Filters

Differentiable particle filters are an emerging class of models that combine sequential Monte Carlo techniques with the flexibility of neural networks to perform state space inference. This paper concerns the case where the system may switch between a finite set of state-space models, i.e. regimes. No prior approaches effectively learn both the individual regimes and the switching process simultaneously. In this paper, we propose the neural network based regime learning differentiable particle filter (RLPF) to address this problem. We further design a training procedure for the RLPF and other related algorithms. We demonstrate competitive performance compared to the previous state-of-the-art algorithms on a pair of numerical experiments.