Statistical Finite Elements via Langevin Dynamics
Paper and Code
Oct 21, 2021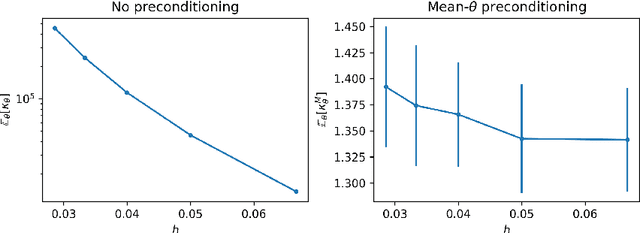

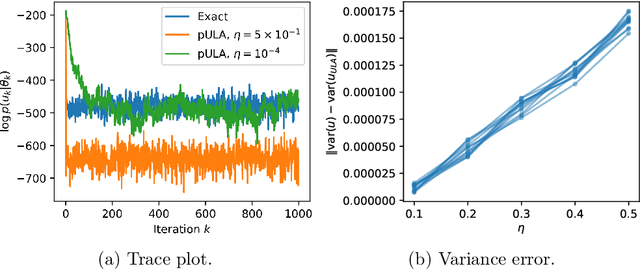
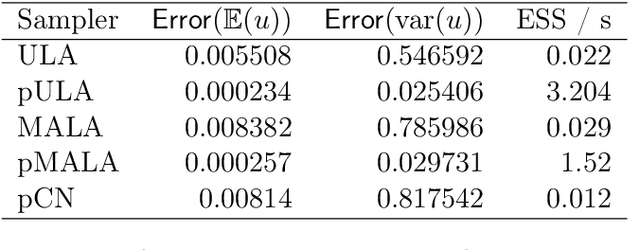
The recent statistical finite element method (statFEM) provides a coherent statistical framework to synthesise finite element models with observed data. Through embedding uncertainty inside of the governing equations, finite element solutions are updated to give a posterior distribution which quantifies all sources of uncertainty associated with the model. However to incorporate all sources of uncertainty, one must integrate over the uncertainty associated with the model parameters, the known forward problem of uncertainty quantification. In this paper, we make use of Langevin dynamics to solve the statFEM forward problem, studying the utility of the unadjusted Langevin algorithm (ULA), a Metropolis-free Markov chain Monte Carlo sampler, to build a sample-based characterisation of this otherwise intractable measure. Due to the structure of the statFEM problem, these methods are able to solve the forward problem without explicit full PDE solves, requiring only sparse matrix-vector products. ULA is also gradient-based, and hence provides a scalable approach up to high degrees-of-freedom. Leveraging the theory behind Langevin-based samplers, we provide theoretical guarantees on sampler performance, demonstrating convergence, for both the prior and posterior, in the Kullback-Leibler divergence, and, in Wasserstein-2, with further results on the effect of preconditioning. Numerical experiments are also provided, for both the prior and posterior, to demonstrate the efficacy of the sampler, with a Python package also included.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge