Multi-view Bayesian optimisation in reduced dimension for engineering design

Bayesian optimisation is an adaptive sampling strategy for constructing a Gaussian process surrogate to emulate a black-box computational model with the aim of efficiently searching for the global minimum. However, Gaussian processes have limited applicability for engineering problems with many design variables. Their scalability can be significantly improved by identifying a low-dimensional vector of latent variables that serve as inputs to the Gaussian process. In this paper, we introduce a multi-view learning strategy that considers both the input design variables and output data representing the objective or constraint functions, to identify a low-dimensional space of latent variables. Adopting a fully probabilistic viewpoint, we use probabilistic partial least squares (PPLS) to learn an orthogonal mapping from the design variables to the latent variables using training data consisting of inputs and outputs of the black-box computational model. The latent variables and posterior probability densities of the probabilistic partial least squares and Gaussian process models are determined sequentially and iteratively, with retraining occurring at each adaptive sampling iteration. We compare the proposed probabilistic partial least squares Bayesian optimisation (PPLS-BO) strategy to its deterministic counterpart, partial least squares Bayesian optimisation (PLS-BO), and classical Bayesian optimisation, demonstrating significant improvements in convergence to the global minimum.

Variational Bayesian surrogate modelling with application to robust design optimisation

Surrogate models provide a quick-to-evaluate approximation to complex computational models and are essential for multi-query problems like design optimisation. The inputs of current computational models are usually high-dimensional and uncertain. We consider Bayesian inference for constructing statistical surrogates with input uncertainties and intrinsic dimensionality reduction. The surrogates are trained by fitting to data from prevalent deterministic computational models. The assumed prior probability density of the surrogate is a Gaussian process. We determine the respective posterior probability density and parameters of the posited statistical model using variational Bayes. The non-Gaussian posterior is approximated by a simpler trial density with free variational parameters and the discrepancy between them is measured using the Kullback-Leibler (KL) divergence. We employ the stochastic gradient method to compute the variational parameters and other statistical model parameters by minimising the KL divergence. We demonstrate the accuracy and versatility of the proposed reduced dimension variational Gaussian process (RDVGP) surrogate on illustrative and robust structural optimisation problems with cost functions depending on a weighted sum of the mean and standard deviation of model outputs.

Stochastic PDE representation of random fields for large-scale Gaussian process regression and statistical finite element analysis

The efficient representation of random fields on geometrically complex domains is crucial for Bayesian modelling in engineering and machine learning. Today's prevalent random field representations are restricted to unbounded domains or are too restrictive in terms of possible field properties. As a result, new techniques leveraging the historically established link between stochastic PDEs (SPDEs) and random fields are especially appealing for engineering applications with complex geometries which already have a finite element discretisation for solving the physical conservation equations. Unlike the dense covariance matrix of a random field, its inverse, the precision matrix, is usually sparse and equal to the stiffness matrix of a Helmholtz-like SPDE. In this paper, we use the SPDE representation to develop a scalable framework for large-scale statistical finite element analysis (statFEM) and Gaussian process (GP) regression on geometrically complex domains. We use the SPDE formulation to obtain the relevant prior probability densities with a sparse precision matrix. The properties of the priors are governed by the parameters and possibly fractional order of the Helmholtz-like SPDE so that we can model on bounded domains and manifolds anisotropic, non-homogeneous random fields with arbitrary smoothness. We use for assembling the sparse precision matrix the same finite element mesh used for solving the physical conservation equations. The observation models for statFEM and GP regression are such that the posterior probability densities are Gaussians with a closed-form mean and precision. The expressions for the mean vector and the precision matrix can be evaluated using only sparse matrix operations. We demonstrate the versatility of the proposed framework and its convergence properties with one and two-dimensional Poisson and thin-shell examples.

Random Grid Neural Processes for Parametric Partial Differential Equations

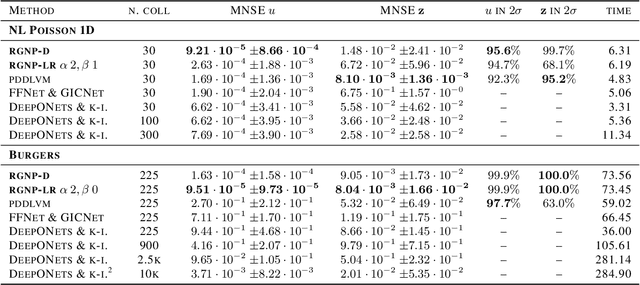
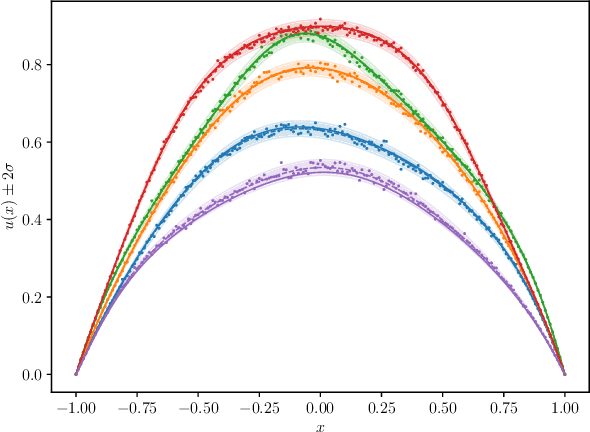
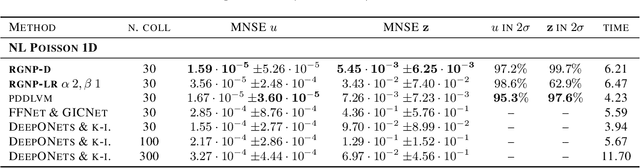
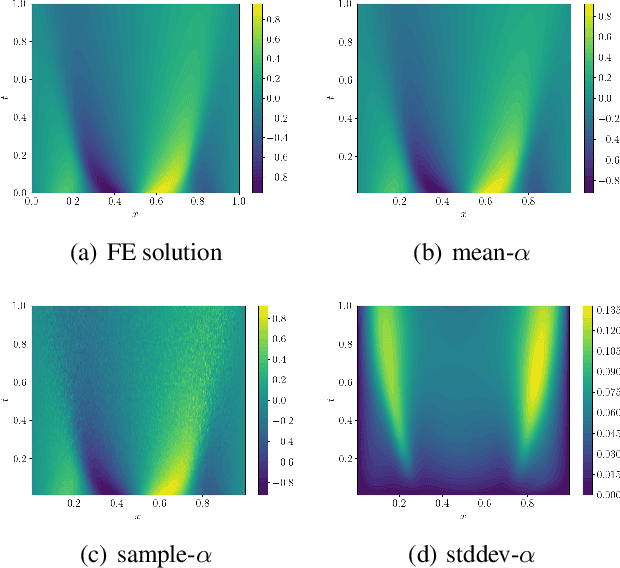
We introduce a new class of spatially stochastic physics and data informed deep latent models for parametric partial differential equations (PDEs) which operate through scalable variational neural processes. We achieve this by assigning probability measures to the spatial domain, which allows us to treat collocation grids probabilistically as random variables to be marginalised out. Adapting this spatial statistics view, we solve forward and inverse problems for parametric PDEs in a way that leads to the construction of Gaussian process models of solution fields. The implementation of these random grids poses a unique set of challenges for inverse physics informed deep learning frameworks and we propose a new architecture called Grid Invariant Convolutional Networks (GICNets) to overcome these challenges. We further show how to incorporate noisy data in a principled manner into our physics informed model to improve predictions for problems where data may be available but whose measurement location does not coincide with any fixed mesh or grid. The proposed method is tested on a nonlinear Poisson problem, Burgers equation, and Navier-Stokes equations, and we provide extensive numerical comparisons. We demonstrate significant computational advantages over current physics informed neural learning methods for parametric PDEs while improving the predictive capabilities and flexibility of these models.

Deep Probabilistic Models for Forward and Inverse Problems in Parametric PDEs

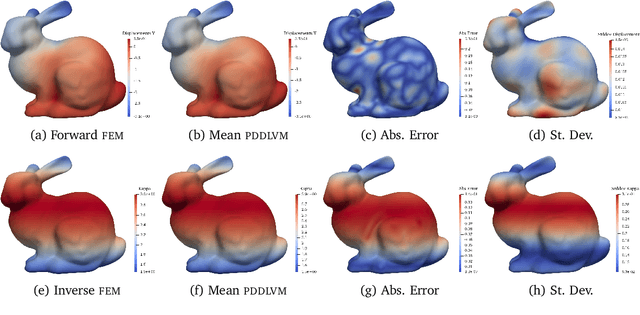
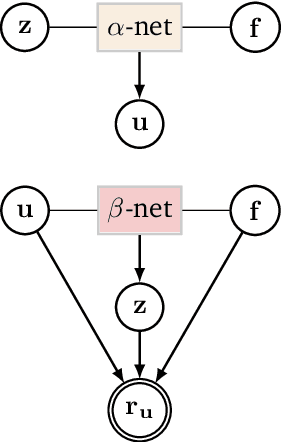
We formulate a class of physics-driven deep latent variable models (PDDLVM) to learn parameter-to-solution (forward) and solution-to-parameter (inverse) maps of parametric partial differential equations (PDEs). Our formulation leverages the finite element method (FEM), deep neural networks, and probabilistic modeling to assemble a deep probabilistic framework in which the forward and inverse maps are approximated with coherent uncertainty quantification. Our probabilistic model explicitly incorporates a parametric PDE-based density and a trainable solution-to-parameter network while the introduced amortized variational family postulates a parameter-to-solution network, all of which are jointly trained. Furthermore, the proposed methodology does not require any expensive PDE solves and is physics-informed only at training time, which allows real-time emulation of PDEs and generation of inverse problem solutions after training, bypassing the need for FEM solve operations with comparable accuracy to FEM solutions. The proposed framework further allows for a seamless integration of observed data for solving inverse problems and building generative models. We demonstrate the effectiveness of our method on a nonlinear Poisson problem, elastic shells with complex 3D geometries, and integrating generic physics-informed neural networks (PINN) architectures. We achieve up to three orders of magnitude speed-ups after training compared to traditional FEM solvers, while outputting coherent uncertainty estimates.

Quaternion variational integration for inertial maneuvering in a biomimetic UAV

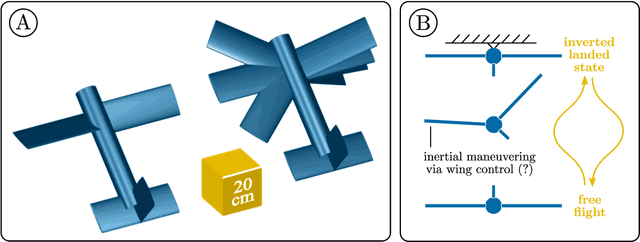
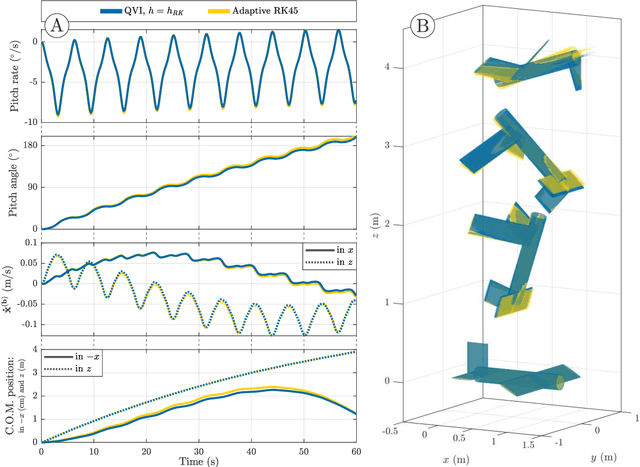
Biological flying, gliding, and falling creatures are capable of extraordinary forms of inertial maneuvering: free-space maneuvering based on fine control of their multibody dynamics, as typified by the self-righting reflexes of cats. However, designing inertial maneuvering capability into biomimetic robots, such as biomimetic unmanned aerial vehicles (UAVs) is challenging. Accurately simulating this maneuvering requires numerical integrators that can ensure both singularity-free integration, and momentum and energy conservation, in a strongly coupled system - properties unavailable in existing conventional integrators. In this work, we develop a pair of novel quaternion variational integrators (QVI) showing these properties, and demonstrate their capability for simulating inertial maneuvering in a biomimetic UAV showing complex multibody-dynamics coupling. Being quaternion-valued, these QVIs are innately singularity-free; and being variational, they can show excellent energy and momentum conservation properties. We explore the effect of variational integration order (left-rectangle vs. midpoint) on the conservation properties of integrator, and conclude that, in complex coupled systems in which canonical momenta may be time-varying, the midpoint integrator is required. The resulting midpoint QVI is well-suited to the analysis of inertial maneuvering in a biomimetic UAV - a feature that we demonstrate in simulation - and of other complex dynamical systems.

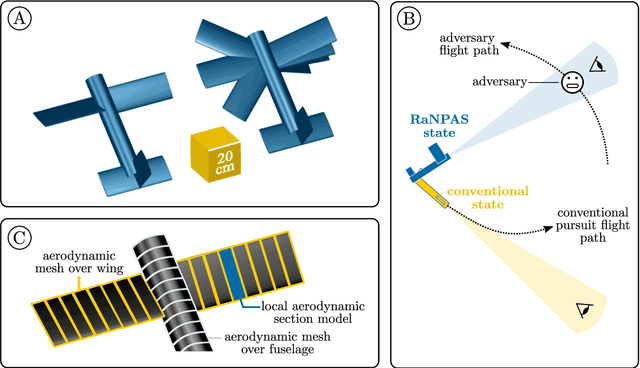
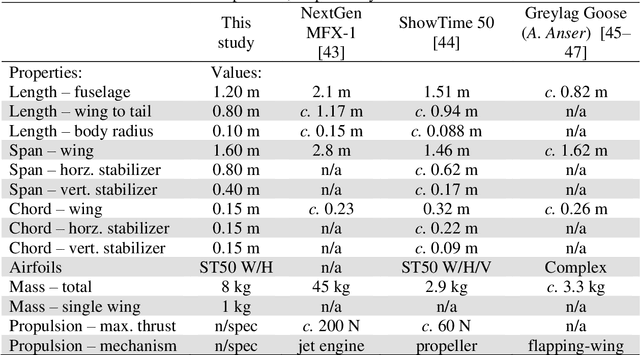
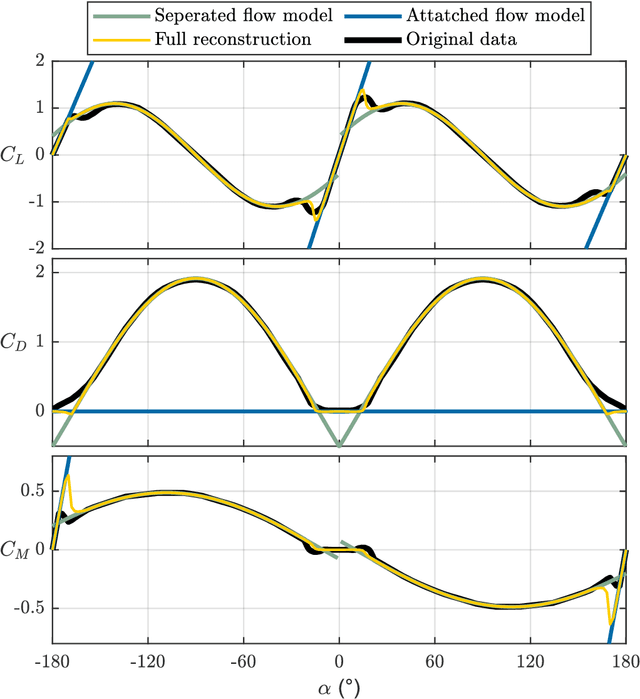
Pitch-axis supermanoeuvrability in a biomimetic morphing-wing aircraft

Birds and bats are extraordinarily adept flyers: whether in hunting prey, or evading predators, their agility and manoeuvrability in flight are characteristics of vital importance. Their performance, in this regard, greatly exceeds that of conventional aircraft. Attempts to close this gap in capability have typically focused on thrust-vectoring technology - the domain of classical supermanoeuvrability - at the expense of biomimicry. In this work, however, we show that these approaches are not incompatible: biomimetic wing morphing is an avenue both to classical supermanoeuvrability, and to new forms of biologically-inspired supermanoeuvrability. Using a state-of-the-art flight simulator, equipped with a multibody model of lifting surface motion and a Goman-Khrabrov dynamic stall model for all lifting surfaces, we demonstrate the capability of a biomimetic morphing-wing unmanned aerial vehicles (UAV) for two key forms of supermanoeuvrability: the Pugachev cobra, and ballistic transition. Conclusions are drawn as to the mechanism by which these manoeuvres can be performed, and their feasibility in practical biomimetic unmanned aerial vehicle (UAV). These conclusions have wide relevance to both the design of supermanoeuvrable UAVs, and the study of biological flight dynamics across multiple species.

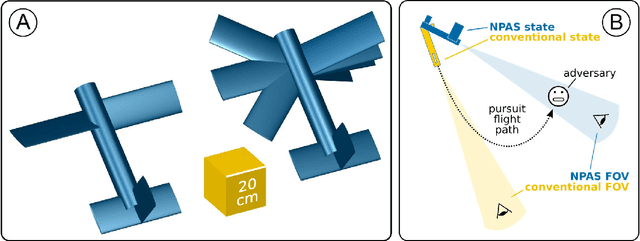
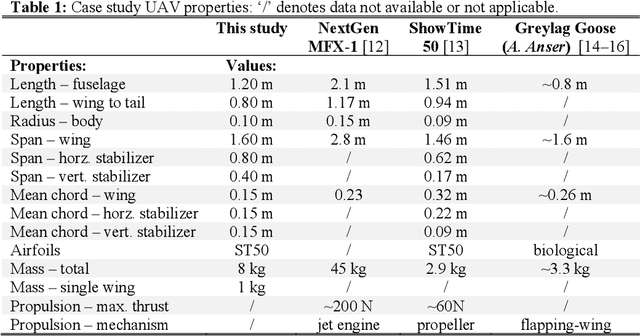
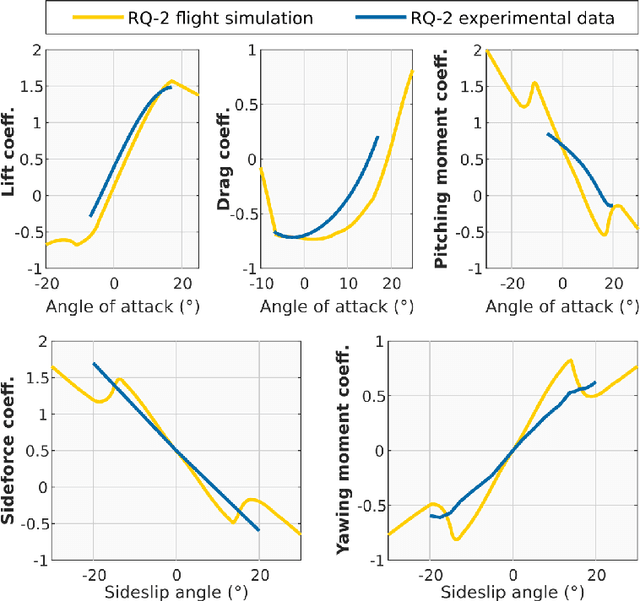
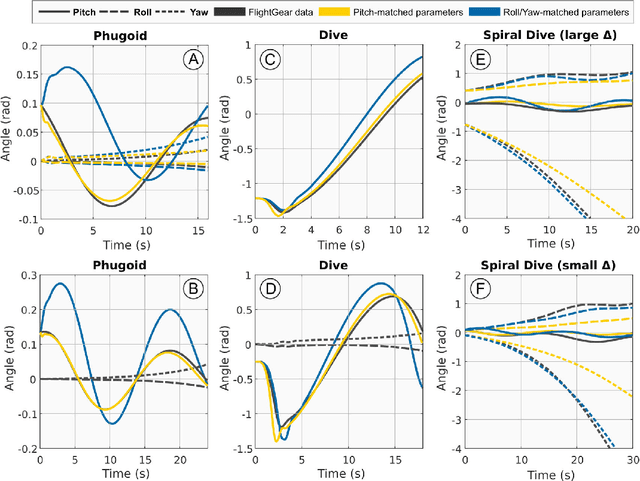
Multiaxis nose-pointing-and-shooting in a biomimetic morphing-wing aircraft

Modern high-performance combat aircraft exceed conventional flight-envelope limits on maneuverability through the use of thrust vectoring, and so achieve supermaneuverability. With ongoing development of biomimetic unmanned aerial vehicles (UAVs), the potential for supermaneuverability through biomimetic mechanisms becomes apparent. So far, this potential has not been well studied: biomimetic UAVs have not yet been shown to be capable of any of the forms of classical supermaneuverability available to thrust-vectored aircraft. Here we show this capability, by demonstrating how biomimetic morphing-wing UAVs can perform sophisticated multiaxis nose-pointing-and-shooting (NPAS) maneuvers at low morphing complexity. Nonlinear flight-dynamic analysis is used to characterize the extent and stability of the multidimensional space of aircraft trim states that arises from biomimetic morphing. Navigating this trim space provides an effective model-based guidance strategy for generating open-loop NPAS maneuvers in simulation. Our results demonstrate the capability of biomimetic aircraft for air combat-relevant supermaneuverability, and provide strategies for the exploration, characterization, and guidance of further forms of classical and non-classical supermaneuverability in such aircraft.

Computational modelling and data-driven homogenisation of knitted membranes

Knitting is an effective technique for producing complex three-dimensional surfaces owing to the inherent flexibility of interlooped yarns and recent advances in manufacturing providing better control of local stitch patterns. Fully yarn-level modelling of large-scale knitted membranes is not feasible. Therefore, we consider a two-scale homogenisation approach and model the membrane as a Kirchhoff-Love shell on the macroscale and as Euler-Bernoulli rods on the microscale. The governing equations for both the shell and the rod are discretised with cubic B-spline basis functions. The solution of the nonlinear microscale problem requires a significant amount of time due to the large deformations and the enforcement of contact constraints, rendering conventional online computational homogenisation approaches infeasible. To sidestep this problem, we use a pre-trained statistical Gaussian Process Regression (GPR) model to map the macroscale deformations to macroscale stresses. During the offline learning phase, the GPR model is trained by solving the microscale problem for a sufficiently rich set of deformation states obtained by either uniform or Sobol sampling. The trained GPR model encodes the nonlinearities and anisotropies present in the microscale and serves as a material model for the macroscale Kirchhoff-Love shell. After verifying and validating the different components of the proposed approach, we introduce several examples involving membranes subjected to tension and shear to demonstrate its versatility and good performance.