Deep Probabilistic Models for Forward and Inverse Problems in Parametric PDEs

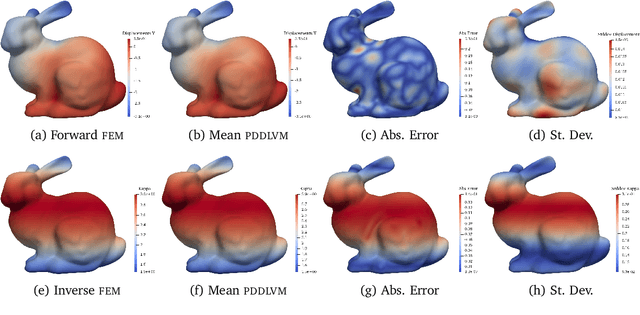
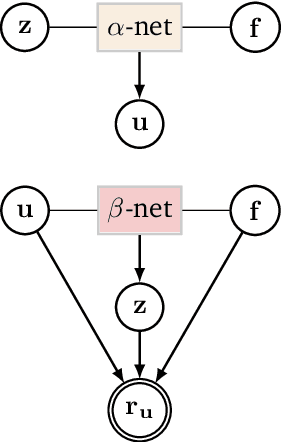
We formulate a class of physics-driven deep latent variable models (PDDLVM) to learn parameter-to-solution (forward) and solution-to-parameter (inverse) maps of parametric partial differential equations (PDEs). Our formulation leverages the finite element method (FEM), deep neural networks, and probabilistic modeling to assemble a deep probabilistic framework in which the forward and inverse maps are approximated with coherent uncertainty quantification. Our probabilistic model explicitly incorporates a parametric PDE-based density and a trainable solution-to-parameter network while the introduced amortized variational family postulates a parameter-to-solution network, all of which are jointly trained. Furthermore, the proposed methodology does not require any expensive PDE solves and is physics-informed only at training time, which allows real-time emulation of PDEs and generation of inverse problem solutions after training, bypassing the need for FEM solve operations with comparable accuracy to FEM solutions. The proposed framework further allows for a seamless integration of observed data for solving inverse problems and building generative models. We demonstrate the effectiveness of our method on a nonlinear Poisson problem, elastic shells with complex 3D geometries, and integrating generic physics-informed neural networks (PINN) architectures. We achieve up to three orders of magnitude speed-ups after training compared to traditional FEM solvers, while outputting coherent uncertainty estimates.