Quaternion variational integration for inertial maneuvering in a biomimetic UAV

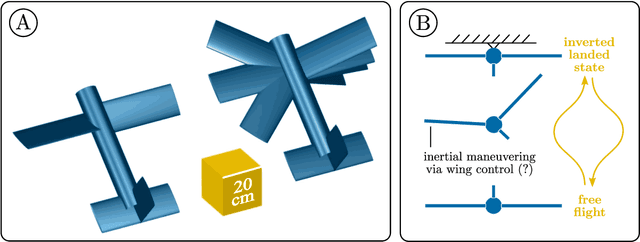
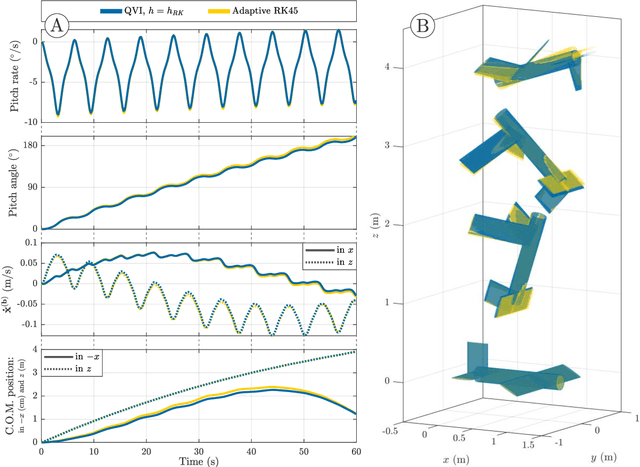
Biological flying, gliding, and falling creatures are capable of extraordinary forms of inertial maneuvering: free-space maneuvering based on fine control of their multibody dynamics, as typified by the self-righting reflexes of cats. However, designing inertial maneuvering capability into biomimetic robots, such as biomimetic unmanned aerial vehicles (UAVs) is challenging. Accurately simulating this maneuvering requires numerical integrators that can ensure both singularity-free integration, and momentum and energy conservation, in a strongly coupled system - properties unavailable in existing conventional integrators. In this work, we develop a pair of novel quaternion variational integrators (QVI) showing these properties, and demonstrate their capability for simulating inertial maneuvering in a biomimetic UAV showing complex multibody-dynamics coupling. Being quaternion-valued, these QVIs are innately singularity-free; and being variational, they can show excellent energy and momentum conservation properties. We explore the effect of variational integration order (left-rectangle vs. midpoint) on the conservation properties of integrator, and conclude that, in complex coupled systems in which canonical momenta may be time-varying, the midpoint integrator is required. The resulting midpoint QVI is well-suited to the analysis of inertial maneuvering in a biomimetic UAV - a feature that we demonstrate in simulation - and of other complex dynamical systems.