Generalized Bayesian Filtering via Sequential Monte Carlo

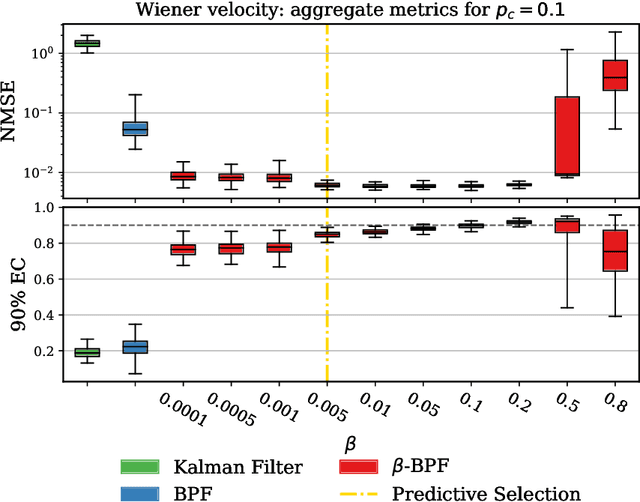
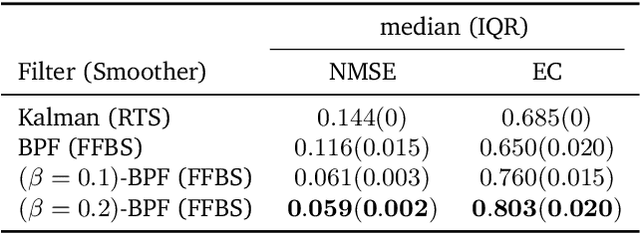
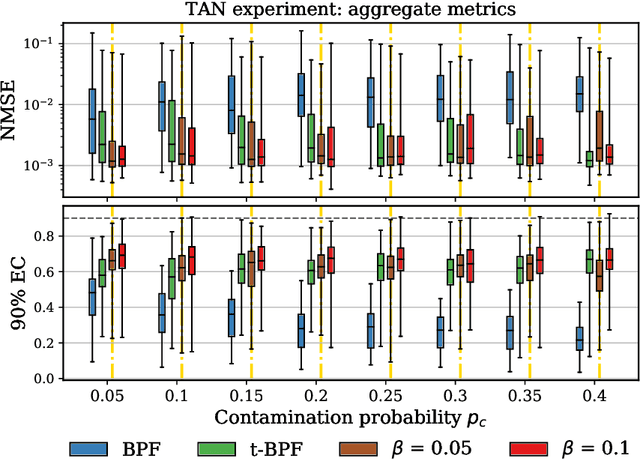
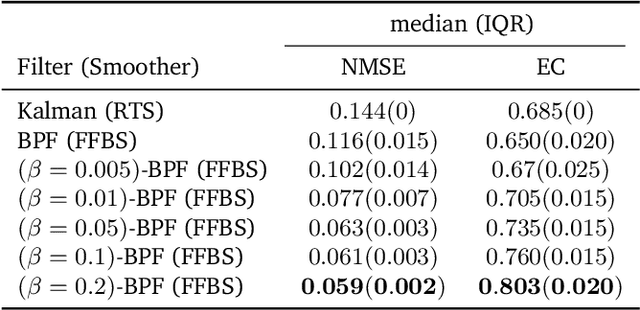
We introduce a framework for inference in general state-space hidden Markov models (HMMs) under likelihood misspecification. In particular, we leverage the loss-theoretic perspective of generalized Bayesian inference (GBI) to define generalized filtering recursions in HMMs, that can tackle the problem of inference under model misspecification. In doing so, we arrive at principled procedures for robust inference against observation contamination through the $\beta$-divergence. Operationalizing the proposed framework is made possible via sequential Monte Carlo methods (SMC). The standard particle methods, and their associated convergence results, are readily generalized to the new setting. We demonstrate our approach to object tracking and Gaussian process regression problems, and observe improved performance over standard filtering algorithms.