Bayes without Underfitting: Fully Correlated Deep Learning Posteriors via Alternating Projections

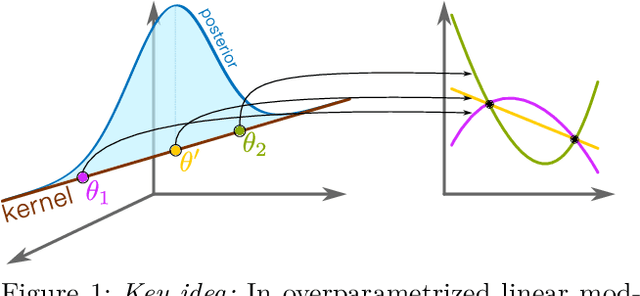
Bayesian deep learning all too often underfits so that the Bayesian prediction is less accurate than a simple point estimate. Uncertainty quantification then comes at the cost of accuracy. For linearized models, the null space of the generalized Gauss-Newton matrix corresponds to parameters that preserve the training predictions of the point estimate. We propose to build Bayesian approximations in this null space, thereby guaranteeing that the Bayesian predictive does not underfit. We suggest a matrix-free algorithm for projecting onto this null space, which scales linearly with the number of parameters and quadratically with the number of output dimensions. We further propose an approximation that only scales linearly with parameters to make the method applicable to generative models. An extensive empirical evaluation shows that the approach scales to large models, including vision transformers with 28 million parameters.

Reparameterization invariance in approximate Bayesian inference

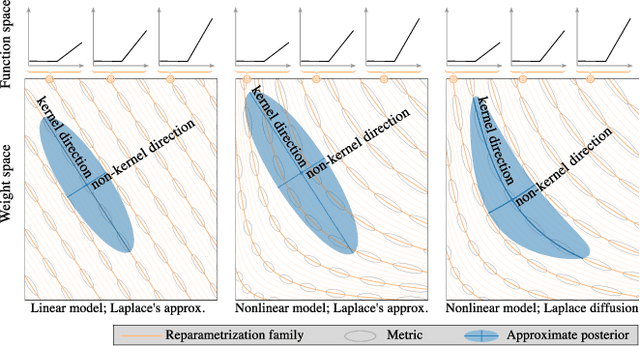
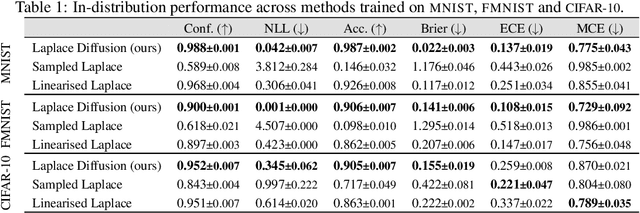
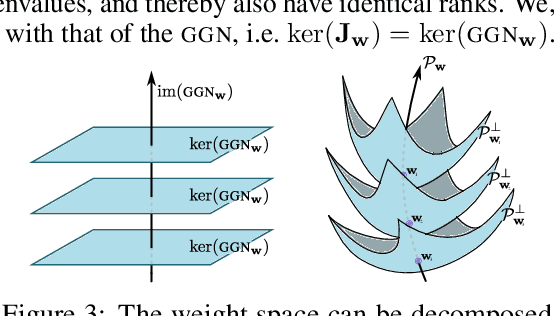
Current approximate posteriors in Bayesian neural networks (BNNs) exhibit a crucial limitation: they fail to maintain invariance under reparameterization, i.e. BNNs assign different posterior densities to different parametrizations of identical functions. This creates a fundamental flaw in the application of Bayesian principles as it breaks the correspondence between uncertainty over the parameters with uncertainty over the parametrized function. In this paper, we investigate this issue in the context of the increasingly popular linearized Laplace approximation. Specifically, it has been observed that linearized predictives alleviate the common underfitting problems of the Laplace approximation. We develop a new geometric view of reparametrizations from which we explain the success of linearization. Moreover, we demonstrate that these reparameterization invariance properties can be extended to the original neural network predictive using a Riemannian diffusion process giving a straightforward algorithm for approximate posterior sampling, which empirically improves posterior fit.

Gradients of Functions of Large Matrices

Tuning scientific and probabilistic machine learning models -- for example, partial differential equations, Gaussian processes, or Bayesian neural networks -- often relies on evaluating functions of matrices whose size grows with the data set or the number of parameters. While the state-of-the-art for evaluating these quantities is almost always based on Lanczos and Arnoldi iterations, the present work is the first to explain how to differentiate these workhorses of numerical linear algebra efficiently. To get there, we derive previously unknown adjoint systems for Lanczos and Arnoldi iterations, implement them in JAX, and show that the resulting code can compete with Diffrax when it comes to differentiating PDEs, GPyTorch for selecting Gaussian process models and beats standard factorisation methods for calibrating Bayesian neural networks. All this is achieved without any problem-specific code optimisation. Find the code at https://github.com/pnkraemer/experiments-lanczos-adjoints and install the library with pip install matfree.

On the curvature of the loss landscape

One of the main challenges in modern deep learning is to understand why such over-parameterized models perform so well when trained on finite data. A way to analyze this generalization concept is through the properties of the associated loss landscape. In this work, we consider the loss landscape as an embedded Riemannian manifold and show that the differential geometric properties of the manifold can be used when analyzing the generalization abilities of a deep net. In particular, we focus on the scalar curvature, which can be computed analytically for our manifold, and show connections to several settings that potentially imply generalization.