Bayes without Underfitting: Fully Correlated Deep Learning Posteriors via Alternating Projections
Paper and Code
Oct 22, 2024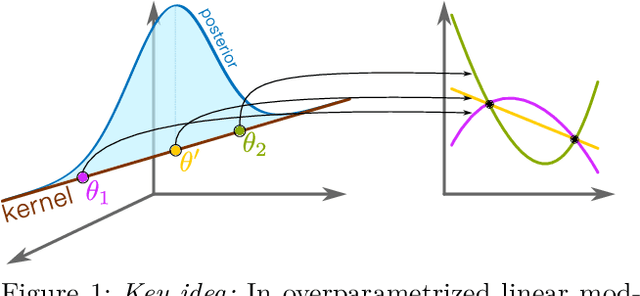



Bayesian deep learning all too often underfits so that the Bayesian prediction is less accurate than a simple point estimate. Uncertainty quantification then comes at the cost of accuracy. For linearized models, the null space of the generalized Gauss-Newton matrix corresponds to parameters that preserve the training predictions of the point estimate. We propose to build Bayesian approximations in this null space, thereby guaranteeing that the Bayesian predictive does not underfit. We suggest a matrix-free algorithm for projecting onto this null space, which scales linearly with the number of parameters and quadratically with the number of output dimensions. We further propose an approximation that only scales linearly with parameters to make the method applicable to generative models. An extensive empirical evaluation shows that the approach scales to large models, including vision transformers with 28 million parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge