Stopping Bayesian Optimization with Probabilistic Regret Bounds

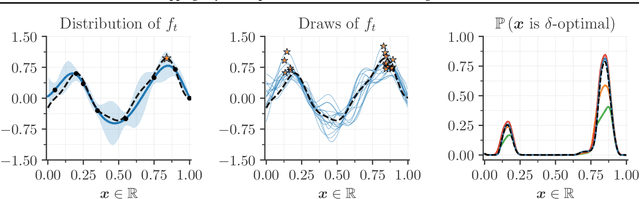
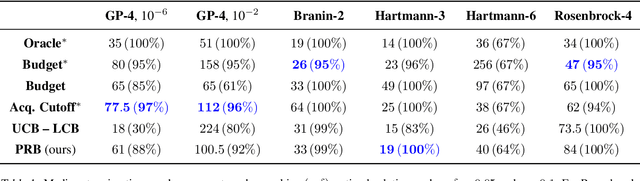
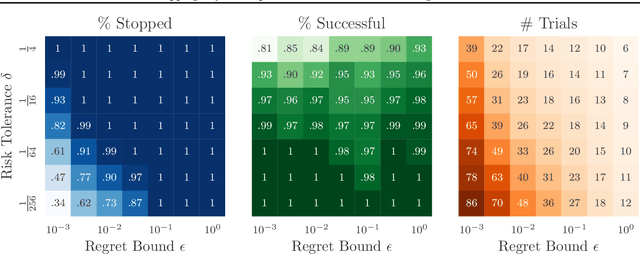
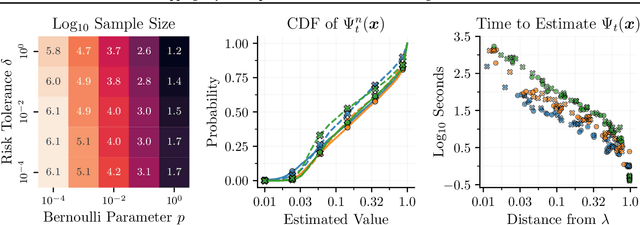
Bayesian optimization is a popular framework for efficiently finding high-quality solutions to difficult problems based on limited prior information. As a rule, these algorithms operate by iteratively choosing what to try next until some predefined budget has been exhausted. We investigate replacing this de facto stopping rule with an $(\epsilon, \delta)$-criterion: stop when a solution has been found whose value is within $\epsilon > 0$ of the optimum with probability at least $1 - \delta$ under the model. Given access to the prior distribution of problems, we show how to verify this condition in practice using a limited number of draws from the posterior. For Gaussian process priors, we prove that Bayesian optimization with the proposed criterion stops in finite time and returns a point that satisfies the $(\epsilon, \delta)$-criterion under mild assumptions. These findings are accompanied by extensive empirical results which demonstrate the strengths and weaknesses of this approach.

A Unifying Variational Framework for Gaussian Process Motion Planning

To control how a robot moves, motion planning algorithms must compute paths in high-dimensional state spaces while accounting for physical constraints related to motors and joints, generating smooth and stable motions, avoiding obstacles, and preventing collisions. A motion planning algorithm must therefore balance competing demands, and should ideally incorporate uncertainty to handle noise, model errors, and facilitate deployment in complex environments. To address these issues, we introduce a framework for robot motion planning based on variational Gaussian Processes, which unifies and generalizes various probabilistic-inference-based motion planning algorithms. Our framework provides a principled and flexible way to incorporate equality-based, inequality-based, and soft motion-planning constraints during end-to-end training, is straightforward to implement, and provides both interval-based and Monte-Carlo-based uncertainty estimates. We conduct experiments using different environments and robots, comparing against baseline approaches based on the feasibility of the planned paths, and obstacle avoidance quality. Results show that our proposed approach yields a good balance between success rates and path quality.

Pathwise Conditioning of Gaussian Processes

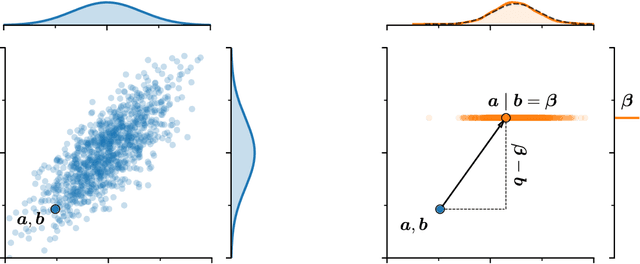
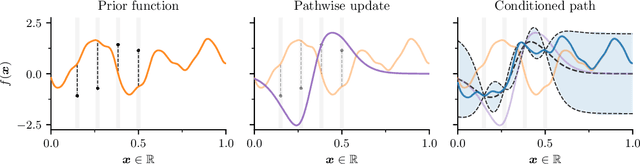
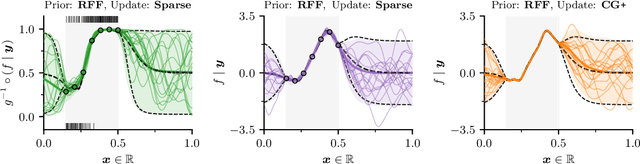
As Gaussian processes are integrated into increasingly complex problem settings, analytic solutions to quantities of interest become scarcer and scarcer. Monte Carlo methods act as a convenient bridge for connecting intractable mathematical expressions with actionable estimates via sampling. Conventional approaches for simulating Gaussian process posteriors view samples as vectors drawn from marginal distributions over process values at a finite number of input location. This distribution-based characterization leads to generative strategies that scale cubically in the size of the desired random vector. These methods are, therefore, prohibitively expensive in cases where high-dimensional vectors - let alone continuous functions - are required. In this work, we investigate a different line of reasoning. Rather than focusing on distributions, we articulate Gaussian conditionals at the level of random variables. We show how this pathwise interpretation of conditioning gives rise to a general family of approximations that lend themselves to fast sampling from Gaussian process posteriors. We analyze these methods, along with the approximation errors they introduce, from first principles. We then complement this theory, by exploring the practical ramifications of pathwise conditioning in a various applied settings.

Efficiently sampling functions from Gaussian process posteriors

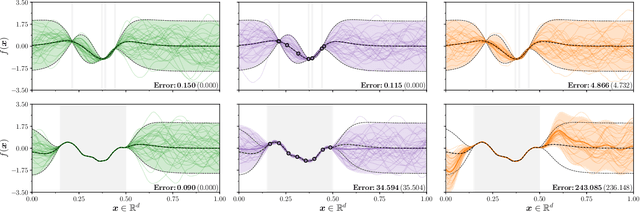
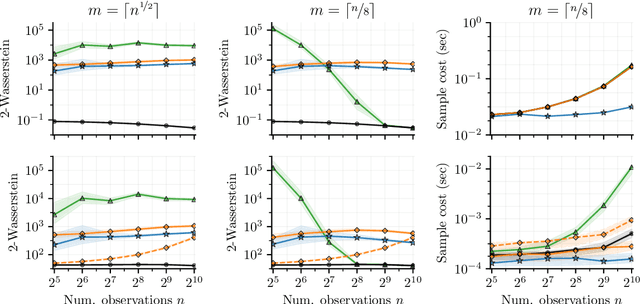
Gaussian processes are the gold standard for many real-world modeling problems, especially in cases where a model's success hinges upon its ability to faithfully represent predictive uncertainty. These problems typically exist as parts of larger frameworks, where quantities of interest are ultimately defined by integrating over posterior distributions. However, these algorithms' inner workings rarely allow for closed-form integration, giving rise to a need for Monte Carlo methods. Despite substantial progress in scaling up Gaussian processes to large training sets, methods for accurately generating draws from their posterior distributions still scale cubically in the number of test locations. We identify a decomposition of Gaussian processes that naturally lends itself to scalable sampling by enabling us to efficiently generate functions that accurately represent their posteriors. Building off of this factorization, we propose decoupled sampling, an easy-to-use and general-purpose approach for fast posterior sampling. Decoupled sampling works as a drop-in strategy that seamlessly pairs with sparse approximations to Gaussian processes to afford scalability both during training and at test time. In a series of experiments designed to test competing sampling schemes' statistical behaviors and practical ramifications, we empirically show that functions drawn using decoupled sampling faithfully represent Gaussian process posteriors at a fraction of the usual cost.

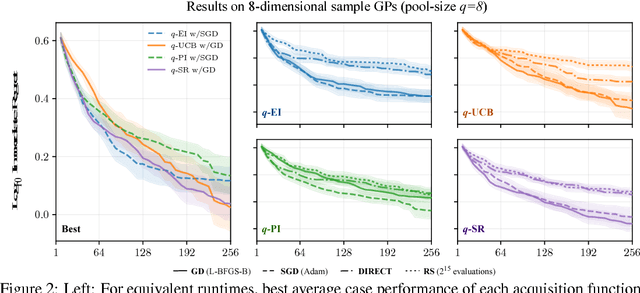
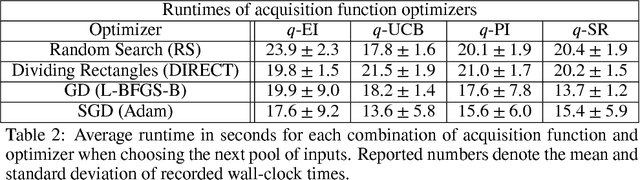
Maximizing acquisition functions for Bayesian optimization

Bayesian optimization is a sample-efficient approach to global optimization that relies on theoretically motivated value heuristics (acquisition functions) to guide the search process. Fully maximizing acquisition functions produces the Bayes' decision rule, but this ideal is difficult to achieve since these functions are frequently non-trivial to optimize. This statement is especially true when evaluating queries in parallel, where acquisition functions are routinely non-convex, high-dimensional, and intractable. We present two modern approaches for maximizing acquisition functions that exploit key properties thereof, namely the differentiability of Monte Carlo integration and the submodularity of parallel querying.

The reparameterization trick for acquisition functions

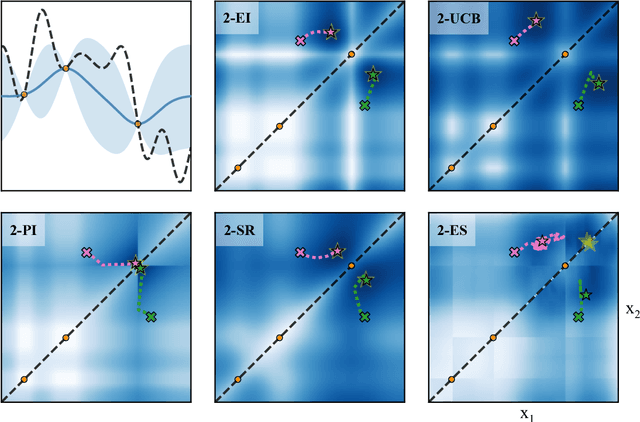
Bayesian optimization is a sample-efficient approach to solving global optimization problems. Along with a surrogate model, this approach relies on theoretically motivated value heuristics (acquisition functions) to guide the search process. Maximizing acquisition functions yields the best performance; unfortunately, this ideal is difficult to achieve since optimizing acquisition functions per se is frequently non-trivial. This statement is especially true in the parallel setting, where acquisition functions are routinely non-convex, high-dimensional, and intractable. Here, we demonstrate how many popular acquisition functions can be formulated as Gaussian integrals amenable to the reparameterization trick and, ensuingly, gradient-based optimization. Further, we use this reparameterized representation to derive an efficient Monte Carlo estimator for the upper confidence bound acquisition function in the context of parallel selection.

Compressing Convolutional Neural Networks

Convolutional neural networks (CNN) are increasingly used in many areas of computer vision. They are particularly attractive because of their ability to "absorb" great quantities of labeled data through millions of parameters. However, as model sizes increase, so do the storage and memory requirements of the classifiers. We present a novel network architecture, Frequency-Sensitive Hashed Nets (FreshNets), which exploits inherent redundancy in both convolutional layers and fully-connected layers of a deep learning model, leading to dramatic savings in memory and storage consumption. Based on the key observation that the weights of learned convolutional filters are typically smooth and low-frequency, we first convert filter weights to the frequency domain with a discrete cosine transform (DCT) and use a low-cost hash function to randomly group frequency parameters into hash buckets. All parameters assigned the same hash bucket share a single value learned with standard back-propagation. To further reduce model size we allocate fewer hash buckets to high-frequency components, which are generally less important. We evaluate FreshNets on eight data sets, and show that it leads to drastically better compressed performance than several relevant baselines.

Compressing Neural Networks with the Hashing Trick

As deep nets are increasingly used in applications suited for mobile devices, a fundamental dilemma becomes apparent: the trend in deep learning is to grow models to absorb ever-increasing data set sizes; however mobile devices are designed with very little memory and cannot store such large models. We present a novel network architecture, HashedNets, that exploits inherent redundancy in neural networks to achieve drastic reductions in model sizes. HashedNets uses a low-cost hash function to randomly group connection weights into hash buckets, and all connections within the same hash bucket share a single parameter value. These parameters are tuned to adjust to the HashedNets weight sharing architecture with standard backprop during training. Our hashing procedure introduces no additional memory overhead, and we demonstrate on several benchmark data sets that HashedNets shrink the storage requirements of neural networks substantially while mostly preserving generalization performance.