The reparameterization trick for acquisition functions
Paper and Code
Dec 01, 2017
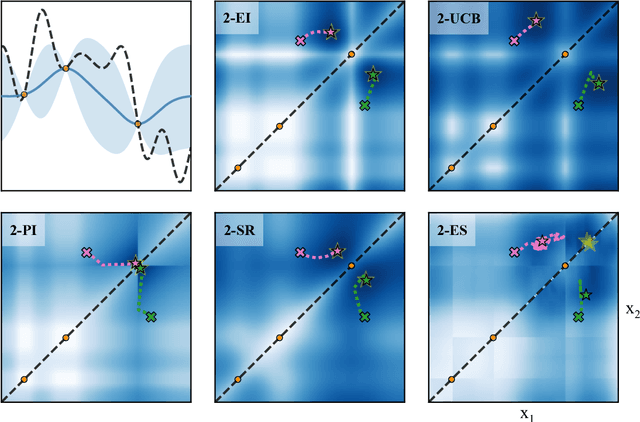
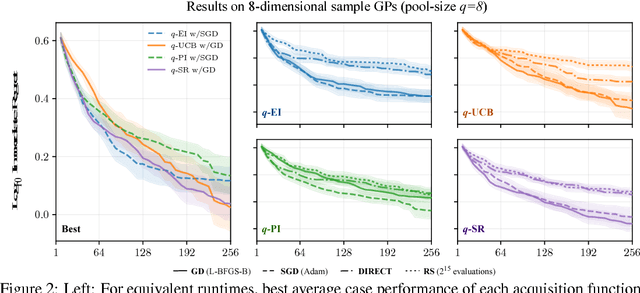
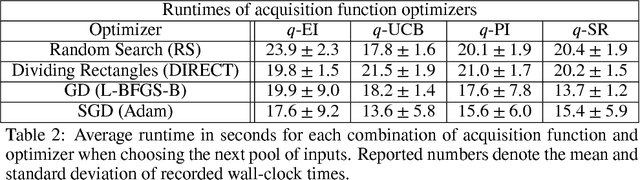
Bayesian optimization is a sample-efficient approach to solving global optimization problems. Along with a surrogate model, this approach relies on theoretically motivated value heuristics (acquisition functions) to guide the search process. Maximizing acquisition functions yields the best performance; unfortunately, this ideal is difficult to achieve since optimizing acquisition functions per se is frequently non-trivial. This statement is especially true in the parallel setting, where acquisition functions are routinely non-convex, high-dimensional, and intractable. Here, we demonstrate how many popular acquisition functions can be formulated as Gaussian integrals amenable to the reparameterization trick and, ensuingly, gradient-based optimization. Further, we use this reparameterized representation to derive an efficient Monte Carlo estimator for the upper confidence bound acquisition function in the context of parallel selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge