Stopping Bayesian Optimization with Probabilistic Regret Bounds
Paper and Code
Feb 26, 2024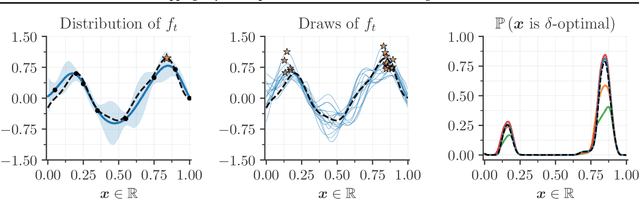
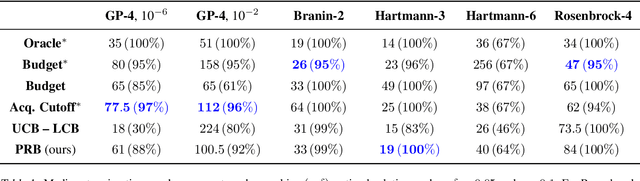
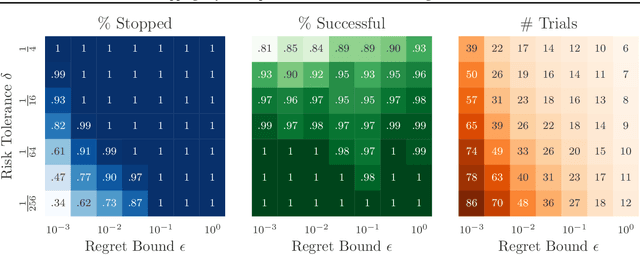
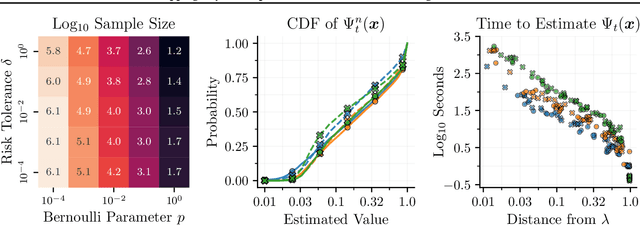
Bayesian optimization is a popular framework for efficiently finding high-quality solutions to difficult problems based on limited prior information. As a rule, these algorithms operate by iteratively choosing what to try next until some predefined budget has been exhausted. We investigate replacing this de facto stopping rule with an $(\epsilon, \delta)$-criterion: stop when a solution has been found whose value is within $\epsilon > 0$ of the optimum with probability at least $1 - \delta$ under the model. Given access to the prior distribution of problems, we show how to verify this condition in practice using a limited number of draws from the posterior. For Gaussian process priors, we prove that Bayesian optimization with the proposed criterion stops in finite time and returns a point that satisfies the $(\epsilon, \delta)$-criterion under mild assumptions. These findings are accompanied by extensive empirical results which demonstrate the strengths and weaknesses of this approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge