Detecting Localized Density Anomalies in Multivariate Data via Coin-Flip Statistics

Detecting localized density differences in multivariate data is a crucial task in computational science. Such anomalies can indicate a critical system failure, lead to a groundbreaking scientific discovery, or reveal unexpected changes in data distribution. We introduce EagleEye, an anomaly detection method to compare two multivariate datasets with the aim of identifying local density anomalies, namely over- or under-densities affecting only localised regions of the feature space. Anomalies are detected by modelling, for each point, the ordered sequence of its neighbours' membership label as a coin-flipping process and monitoring deviations from the expected behaviour of such process. A unique advantage of our method is its ability to provide an accurate, entirely unsupervised estimate of the local signal purity. We demonstrate its effectiveness through experiments on both synthetic and real-world datasets. In synthetic data, EagleEye accurately detects anomalies in multiple dimensions even when they affect a tiny fraction of the data. When applied to a challenging resonant anomaly detection benchmark task in simulated Large Hadron Collider data, EagleEye successfully identifies particle decay events present in just 0.3% of the dataset. In global temperature data, EagleEye uncovers previously unidentified, geographically localised changes in temperature fields that occurred in the most recent years. Thanks to its key advantages of conceptual simplicity, computational efficiency, trivial parallelisation, and scalability, EagleEye is widely applicable across many fields.

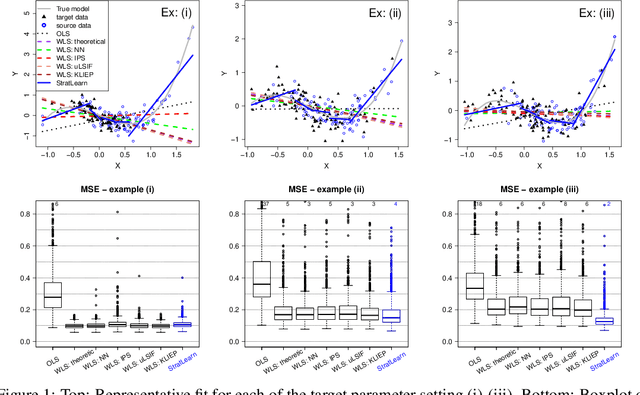
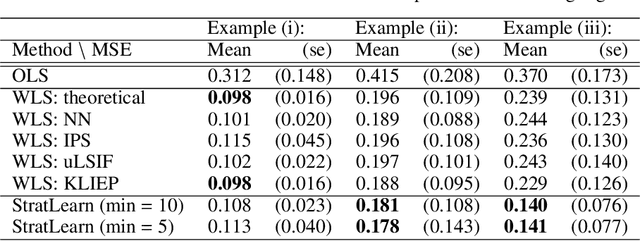
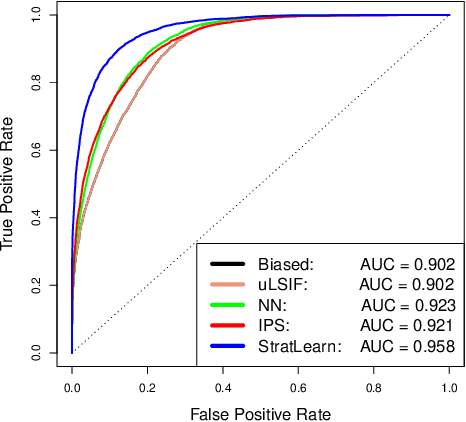
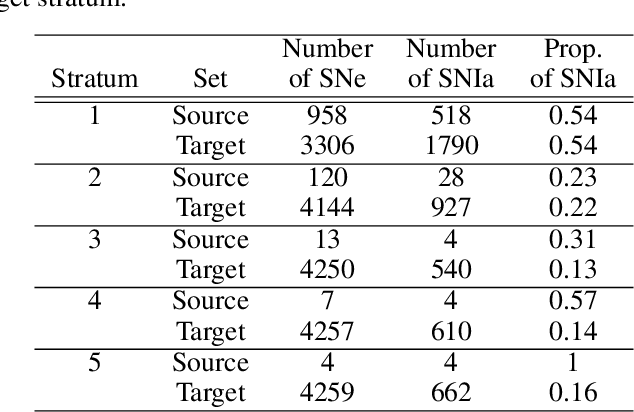
Stratified Learning: a general-purpose statistical method for improved learning under Covariate Shift

Covariate shift arises when the labelled training (source) data is not representative of the unlabelled (target) data due to systematic differences in the covariate distributions. A supervised model trained on the source data subject to covariate shift may suffer from poor generalization on the target data. We propose a novel, statistically principled and theoretically justified method to improve learning under covariate shift conditions, based on propensity score stratification, a well-established methodology in causal inference. We show that the effects of covariate shift can be reduced or altogether eliminated by conditioning on propensity scores. In practice, this is achieved by fitting learners on subgroups ("strata") constructed by partitioning the data based on the estimated propensity scores, leading to balanced covariates and much-improved target prediction. We demonstrate the effectiveness of our general-purpose method on contemporary research questions in observational cosmology, and on additional benchmark examples, matching or outperforming state-of-the-art importance weighting methods, widely studied in the covariate shift literature. We obtain the best reported AUC (0.958) on the updated "Supernovae photometric classification challenge" and improve upon existing conditional density estimation of galaxy redshift from Sloan Data Sky Survey (SDSS) data.