GenCtrl -- A Formal Controllability Toolkit for Generative Models

As generative models become ubiquitous, there is a critical need for fine-grained control over the generation process. Yet, while controlled generation methods from prompting to fine-tuning proliferate, a fundamental question remains unanswered: are these models truly controllable in the first place? In this work, we provide a theoretical framework to formally answer this question. Framing human-model interaction as a control process, we propose a novel algorithm to estimate the controllable sets of models in a dialogue setting. Notably, we provide formal guarantees on the estimation error as a function of sample complexity: we derive probably-approximately correct bounds for controllable set estimates that are distribution-free, employ no assumptions except for output boundedness, and work for any black-box nonlinear control system (i.e., any generative model). We empirically demonstrate the theoretical framework on different tasks in controlling dialogue processes, for both language models and text-to-image generation. Our results show that model controllability is surprisingly fragile and highly dependent on the experimental setting. This highlights the need for rigorous controllability analysis, shifting the focus from simply attempting control to first understanding its fundamental limits.

Tracing the complexity profiles of different linguistic phenomena through the intrinsic dimension of LLM representations

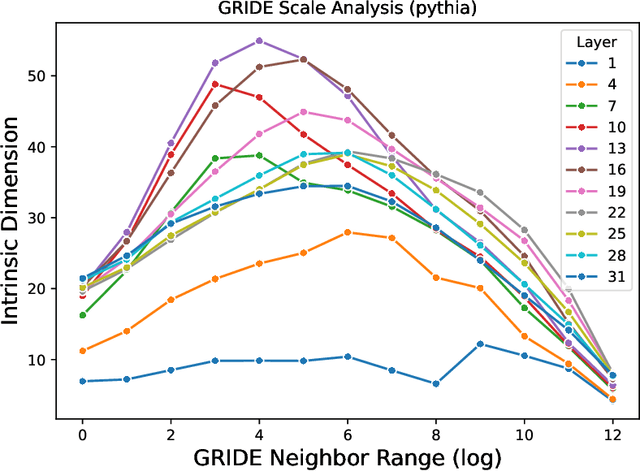
We explore the intrinsic dimension (ID) of LLM representations as a marker of linguistic complexity, asking if different ID profiles across LLM layers differentially characterize formal and functional complexity. We find the formal contrast between sentences with multiple coordinated or subordinated clauses to be reflected in ID differences whose onset aligns with a phase of more abstract linguistic processing independently identified in earlier work. The functional contrasts between sentences characterized by right branching vs. center embedding or unambiguous vs. ambiguous relative clause attachment are also picked up by ID, but in a less marked way, and they do not correlate with the same processing phase. Further experiments using representational similarity and layer ablation confirm the same trends. We conclude that ID is a useful marker of linguistic complexity in LLMs, that it allows to differentiate between different types of complexity, and that it points to similar stages of linguistic processing across disparate LLMs.

Principles of semantic and functional efficiency in grammatical patterning

Grammatical features such as number and gender serve two central functions in human languages. While they encode salient semantic attributes like numerosity and animacy, they also offload sentence processing cost by predictably linking words together via grammatical agreement. Grammars exhibit consistent organizational patterns across diverse languages, invariably rooted in a semantic foundation, a widely confirmed but still theoretically unexplained phenomenon. To explain the basis of universal grammatical patterns, we unify two fundamental properties of grammar, semantic encoding and agreement-based predictability, into a single information-theoretic objective under cognitive constraints. Our analyses reveal that grammatical organization provably inherits from perceptual attributes, but that grammars empirically prioritize functional goals, promoting efficient language processing over semantic encoding.

Geometric Signatures of Compositionality Across a Language Model's Lifetime

Compositionality, the notion that the meaning of an expression is constructed from the meaning of its parts and syntactic rules, permits the infinite productivity of human language. For the first time, artificial language models (LMs) are able to match human performance in a number of compositional generalization tasks. However, much remains to be understood about the representational mechanisms underlying these abilities. We take a high-level geometric approach to this problem by relating the degree of compositionality in a dataset to the intrinsic dimensionality of its representations under an LM, a measure of feature complexity. We find not only that the degree of dataset compositionality is reflected in representations' intrinsic dimensionality, but that the relationship between compositionality and geometric complexity arises due to learned linguistic features over training. Finally, our analyses reveal a striking contrast between linear and nonlinear dimensionality, showing that they respectively encode formal and semantic aspects of linguistic composition.

Evidence from fMRI Supports a Two-Phase Abstraction Process in Language Models

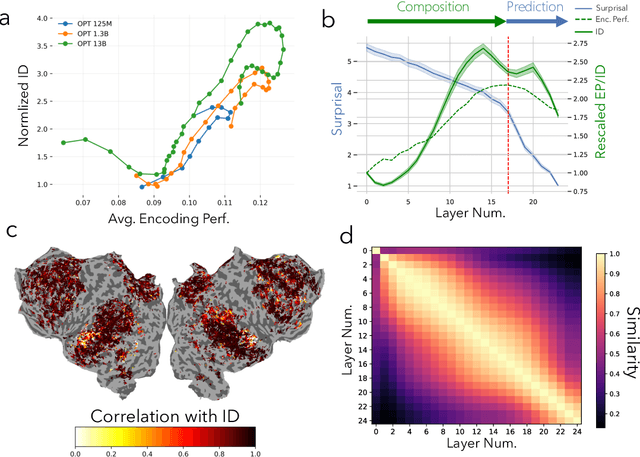
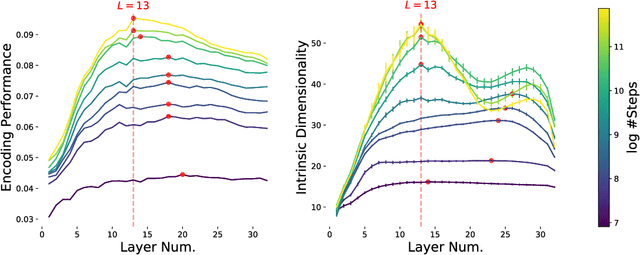
Research has repeatedly demonstrated that intermediate hidden states extracted from large language models are able to predict measured brain response to natural language stimuli. Yet, very little is known about the representation properties that enable this high prediction performance. Why is it the intermediate layers, and not the output layers, that are most capable for this unique and highly general transfer task? In this work, we show that evidence from language encoding models in fMRI supports the existence of a two-phase abstraction process within LLMs. We use manifold learning methods to show that this abstraction process naturally arises over the course of training a language model and that the first "composition" phase of this abstraction process is compressed into fewer layers as training continues. Finally, we demonstrate a strong correspondence between layerwise encoding performance and the intrinsic dimensionality of representations from LLMs. We give initial evidence that this correspondence primarily derives from the inherent compositionality of LLMs and not their next-word prediction properties.

Linearly Controlled Language Generation with Performative Guarantees

The increasing prevalence of Large Language Models (LMs) in critical applications highlights the need for controlled language generation strategies that are not only computationally efficient but that also enjoy performance guarantees. To achieve this, we use a common model of concept semantics as linearly represented in an LM's latent space. In particular, we take the view that natural language generation traces a trajectory in this continuous semantic space, realized by the language model's hidden activations. This view permits a control-theoretic treatment of text generation in latent space, in which we propose a lightweight, gradient-free intervention that dynamically steers trajectories away from regions corresponding to undesired meanings. Crucially, we show that this intervention, which we compute in closed form, is guaranteed (in probability) to steer the output into the allowed region. Finally, we demonstrate on a toxicity avoidance objective that the intervention steers language away from undesired content while maintaining text quality.

Emergence of a High-Dimensional Abstraction Phase in Language Transformers

A language model (LM) is a mapping from a linguistic context to an output token. However, much remains to be known about this mapping, including how its geometric properties relate to its function. We take a high-level geometric approach to its analysis, observing, across five pre-trained transformer-based LMs and three input datasets, a distinct phase characterized by high intrinsic dimensionality. During this phase, representations (1) correspond to the first full linguistic abstraction of the input; (2) are the first to viably transfer to downstream tasks; (3) predict each other across different LMs. Moreover, we find that an earlier onset of the phase strongly predicts better language modelling performance. In short, our results suggest that a central high-dimensionality phase underlies core linguistic processing in many common LM architectures.

Bridging Information-Theoretic and Geometric Compression in Language Models

For a language model (LM) to faithfully model human language, it must compress vast, potentially infinite information into relatively few dimensions. We propose analyzing compression in (pre-trained) LMs from two points of view: geometric and information-theoretic. We demonstrate that the two views are highly correlated, such that the intrinsic geometric dimension of linguistic data predicts their coding length under the LM. We then show that, in turn, high compression of a linguistic dataset predicts rapid adaptation to that dataset, confirming that being able to compress linguistic information is an important part of successful LM performance. As a practical byproduct of our analysis, we evaluate a battery of intrinsic dimension estimators for the first time on linguistic data, showing that only some encapsulate the relationship between information-theoretic compression, geometric compression, and ease-of-adaptation.

On the Correspondence between Compositionality and Imitation in Emergent Neural Communication

Compositionality is a hallmark of human language that not only enables linguistic generalization, but also potentially facilitates acquisition. When simulating language emergence with neural networks, compositionality has been shown to improve communication performance; however, its impact on imitation learning has yet to be investigated. Our work explores the link between compositionality and imitation in a Lewis game played by deep neural agents. Our contributions are twofold: first, we show that the learning algorithm used to imitate is crucial: supervised learning tends to produce more average languages, while reinforcement learning introduces a selection pressure toward more compositional languages. Second, our study reveals that compositional languages are easier to imitate, which may induce the pressure toward compositional languages in RL imitation settings.