Representation mitosis in wide neural networks
Paper and Code
Jun 07, 2021
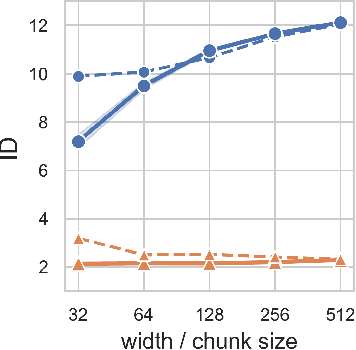
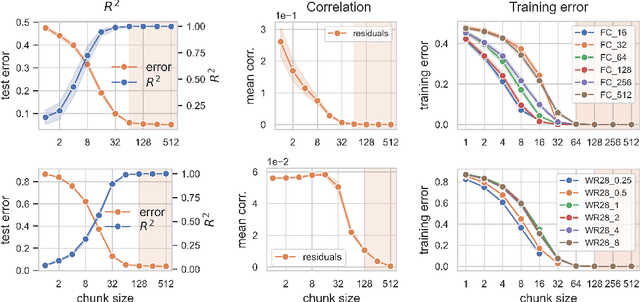
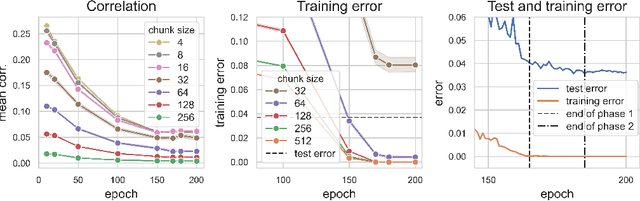
Deep neural networks (DNNs) defy the classical bias-variance trade-off: adding parameters to a DNN that exactly interpolates its training data will typically improve its generalisation performance. Explaining the mechanism behind the benefit of such over-parameterisation is an outstanding challenge for deep learning theory. Here, we study the last layer representation of various deep architectures such as Wide-ResNets for image classification and find evidence for an underlying mechanism that we call *representation mitosis*: if the last hidden representation is wide enough, its neurons tend to split into groups which carry identical information, and differ from each other only by a statistically independent noise. Like in a mitosis process, the number of such groups, or ``clones'', increases linearly with the width of the layer, but only if the width is above a critical value. We show that a key ingredient to activate mitosis is continuing the training process until the training error is zero. Finally, we show that in one of the learning tasks we considered, a wide model with several automatically developed clones performs significantly better than a deep ensemble based on architectures in which the last layer has the same size as the clones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge