Addressing Class Imbalance in Classification Problems of Noisy Signals by using Fourier Transform Surrogates

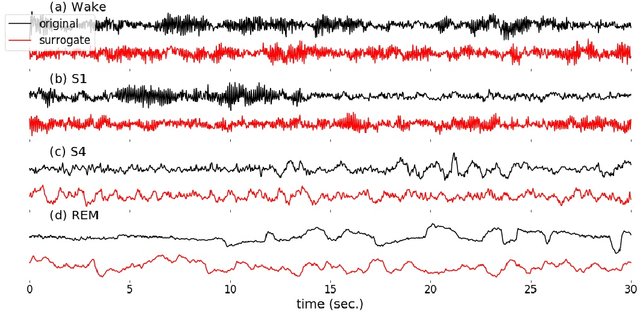
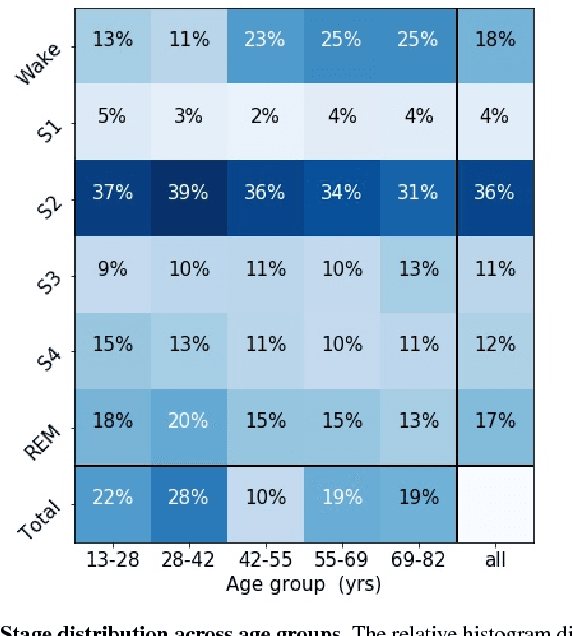
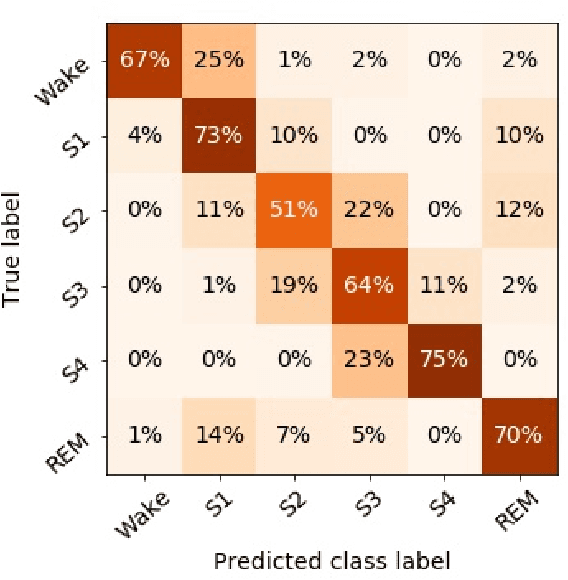
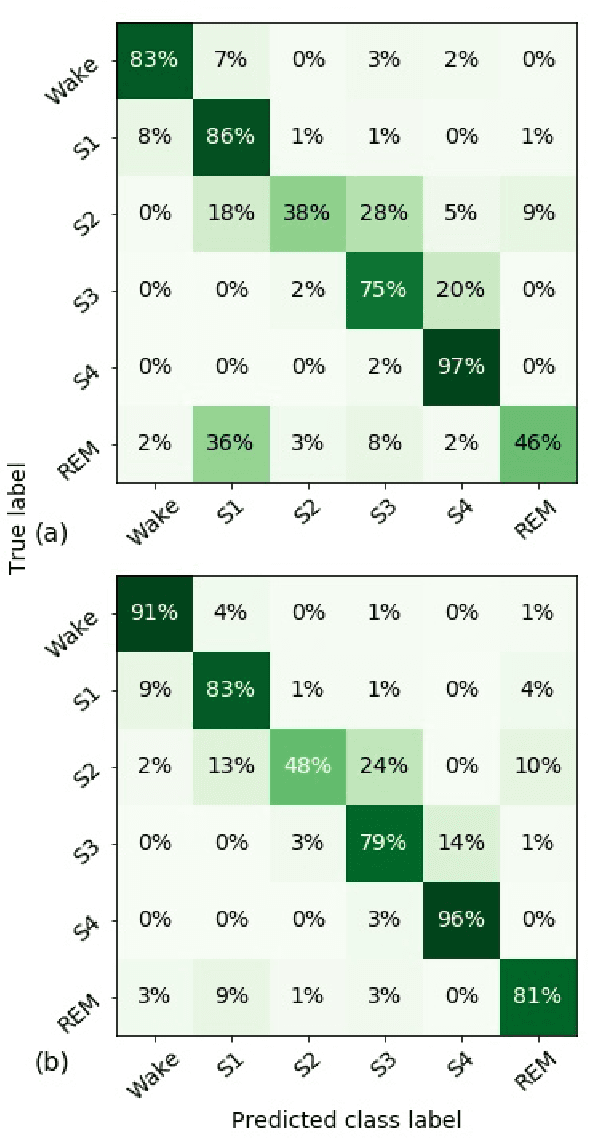
Randomizing the Fourier-transform (FT) phases of temporal-spatial data generates surrogates that approximate examples from the data-generating distribution. We propose such FT surrogates as a novel tool to augment and analyze training of neural networks and explore the approach in the example of sleep-stage classification. By computing FT surrogates of raw EEG, EOG, and EMG signals of under-represented sleep stages, we balanced the CAPSLPDB sleep database. We then trained and tested a convolutional neural network for sleep stage classification, and found that our surrogate-based augmentation improved the mean F1-score by 7%. As another application of FT surrogates, we formulated an approach to compute saliency maps for individual sleep epochs. The visualization is based on the response of inferred class probabilities under replacement of short data segments by partial surrogates. To quantify how well the distributions of the surrogates and the original data match, we evaluated a trained classifier on surrogates of correctly classified examples, and summarized these conditional predictions in a confusion matrix. We show how such conditional confusion matrices can qualitatively explain the performance of surrogates in class balancing. The FT-surrogate augmentation approach may improve classification on noisy signals if carefully adapted to the data distribution under analysis.

Understanding Machine-learned Density Functionals

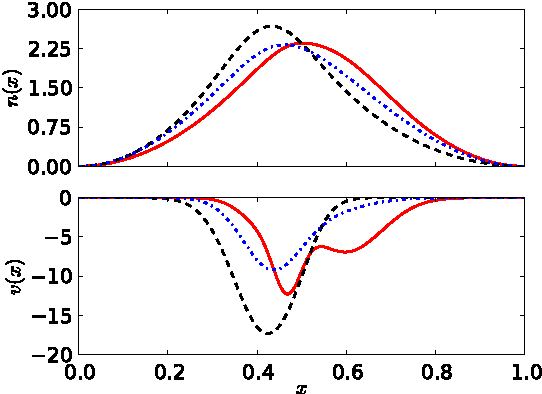
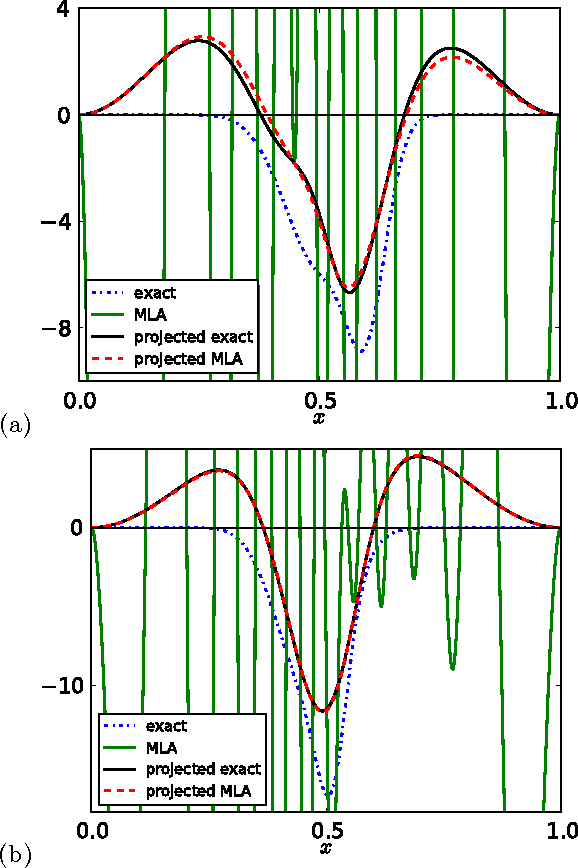
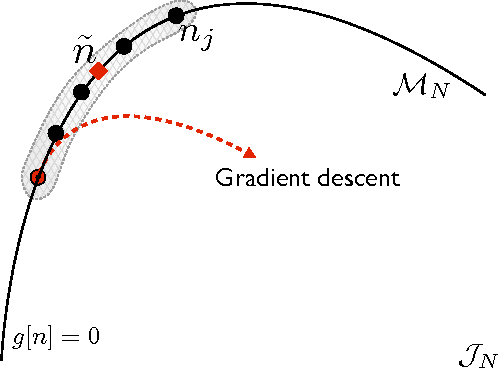
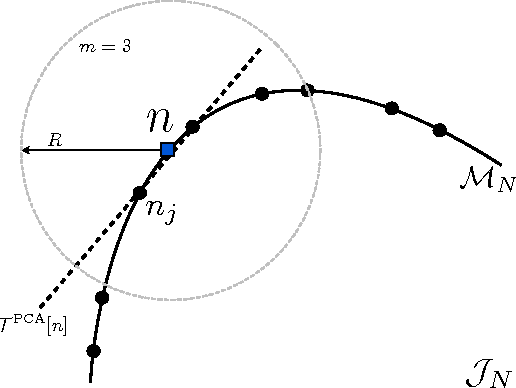
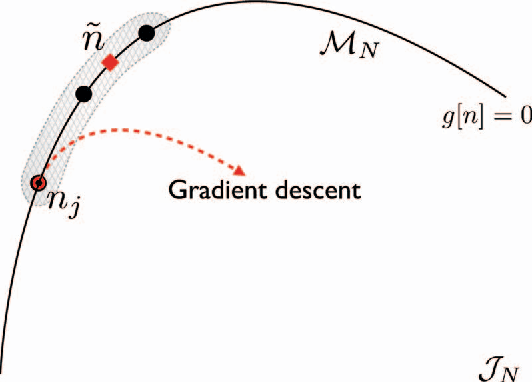
Kernel ridge regression is used to approximate the kinetic energy of non-interacting fermions in a one-dimensional box as a functional of their density. The properties of different kernels and methods of cross-validation are explored, and highly accurate energies are achieved. Accurate {\em constrained optimal densities} are found via a modified Euler-Lagrange constrained minimization of the total energy. A projected gradient descent algorithm is derived using local principal component analysis. Additionally, a sparse grid representation of the density can be used without degrading the performance of the methods. The implications for machine-learned density functional approximations are discussed.

Orbital-free Bond Breaking via Machine Learning

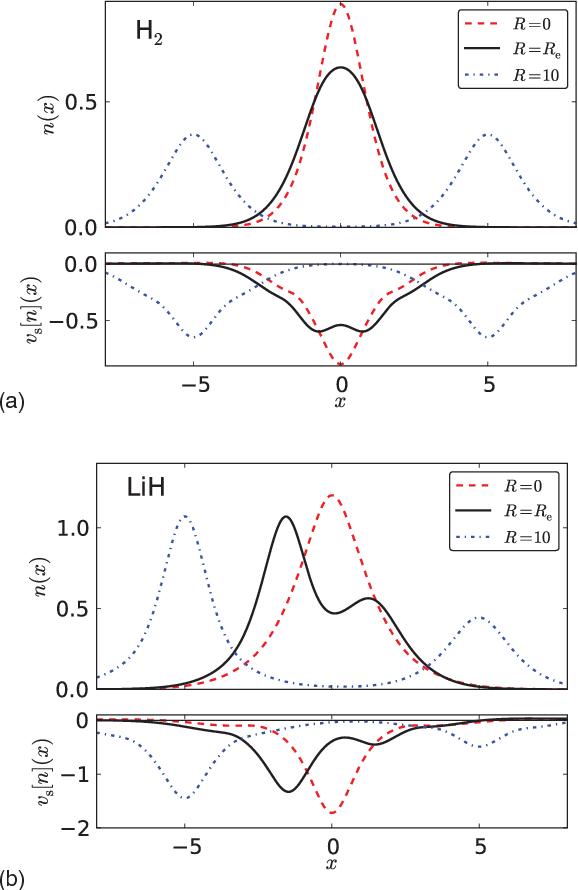
Machine learning is used to approximate the kinetic energy of one dimensional diatomics as a functional of the electron density. The functional can accurately dissociate a diatomic, and can be systematically improved with training. Highly accurate self-consistent densities and molecular forces are found, indicating the possibility for ab-initio molecular dynamics simulations.

Finding Density Functionals with Machine Learning

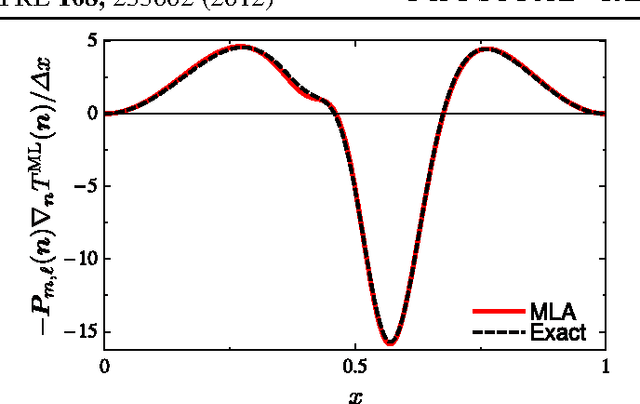
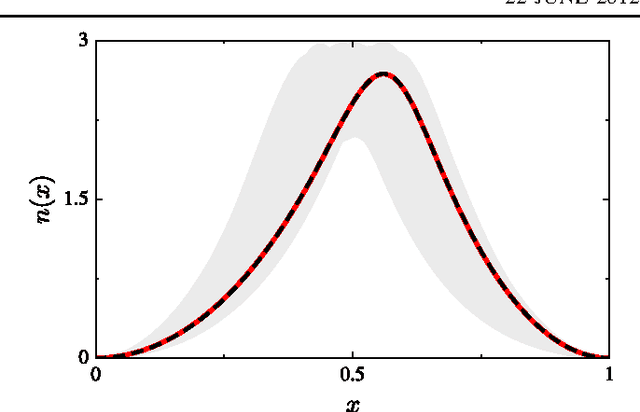
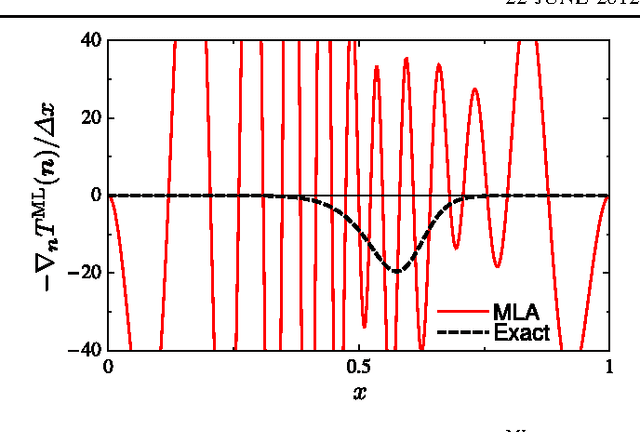
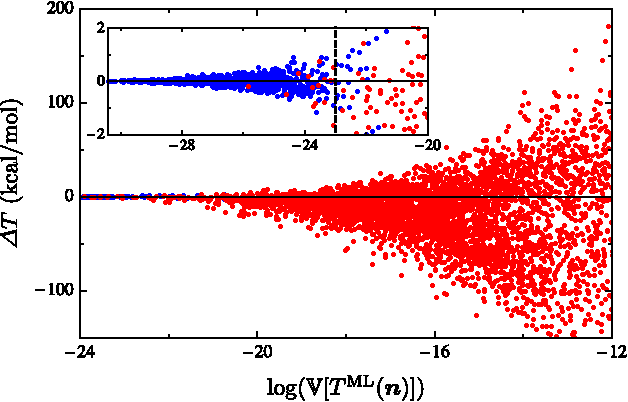
Machine learning is used to approximate density functionals. For the model problem of the kinetic energy of non-interacting fermions in 1d, mean absolute errors below 1 kcal/mol on test densities similar to the training set are reached with fewer than 100 training densities. A predictor identifies if a test density is within the interpolation region. Via principal component analysis, a projected functional derivative finds highly accurate self-consistent densities. Challenges for application of our method to real electronic structure problems are discussed.