Addressing Class Imbalance in Classification Problems of Noisy Signals by using Fourier Transform Surrogates
Paper and Code
Jun 20, 2018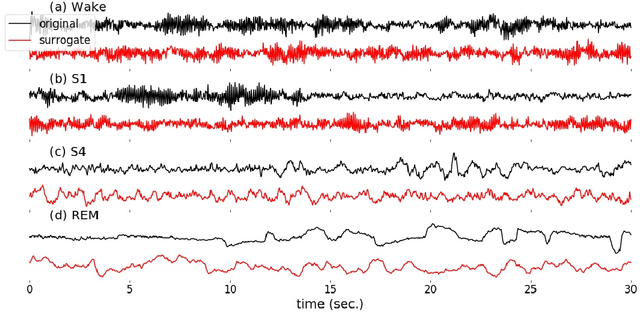
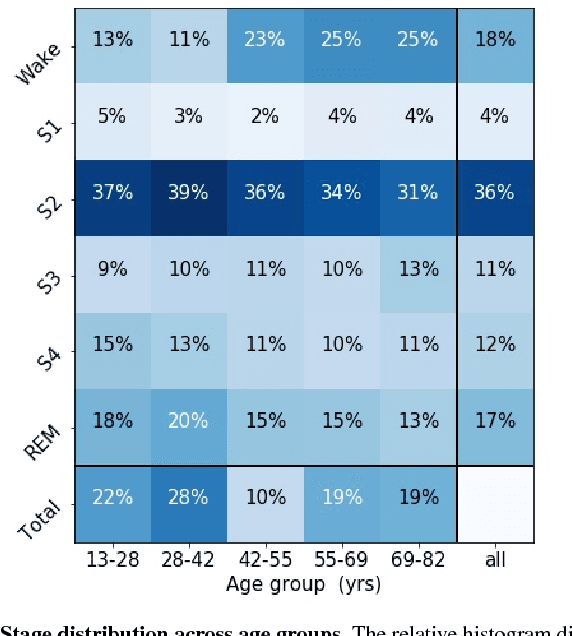
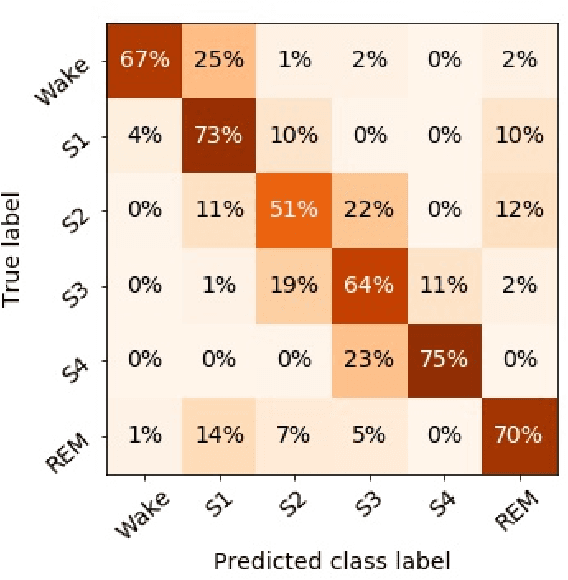
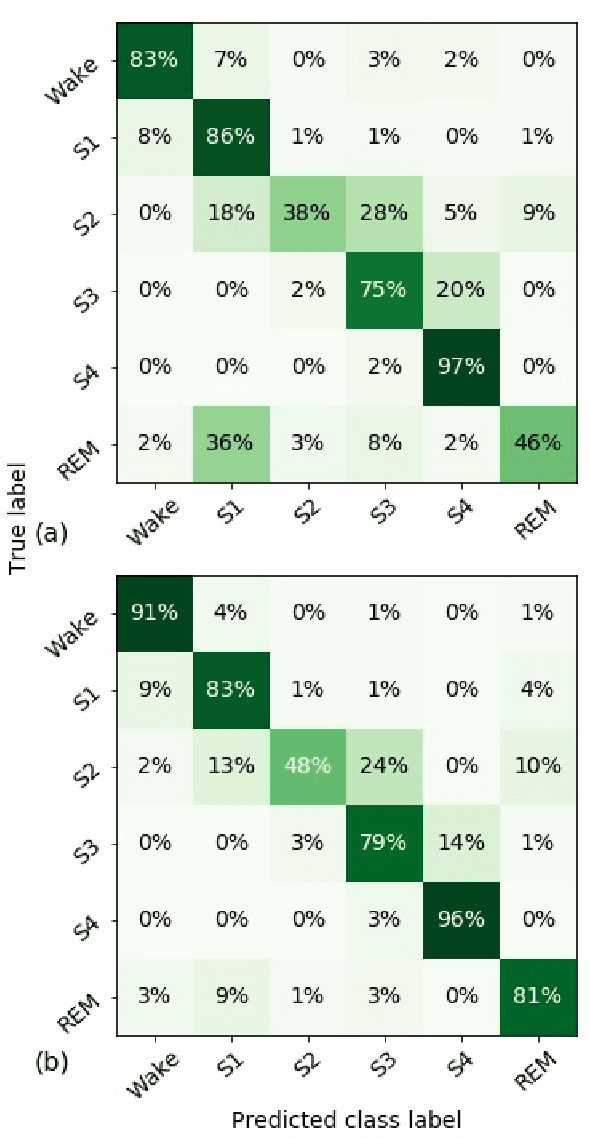
Randomizing the Fourier-transform (FT) phases of temporal-spatial data generates surrogates that approximate examples from the data-generating distribution. We propose such FT surrogates as a novel tool to augment and analyze training of neural networks and explore the approach in the example of sleep-stage classification. By computing FT surrogates of raw EEG, EOG, and EMG signals of under-represented sleep stages, we balanced the CAPSLPDB sleep database. We then trained and tested a convolutional neural network for sleep stage classification, and found that our surrogate-based augmentation improved the mean F1-score by 7%. As another application of FT surrogates, we formulated an approach to compute saliency maps for individual sleep epochs. The visualization is based on the response of inferred class probabilities under replacement of short data segments by partial surrogates. To quantify how well the distributions of the surrogates and the original data match, we evaluated a trained classifier on surrogates of correctly classified examples, and summarized these conditional predictions in a confusion matrix. We show how such conditional confusion matrices can qualitatively explain the performance of surrogates in class balancing. The FT-surrogate augmentation approach may improve classification on noisy signals if carefully adapted to the data distribution under analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge