Towards CRISP-ML: A Machine Learning Process Model with Quality Assurance Methodology

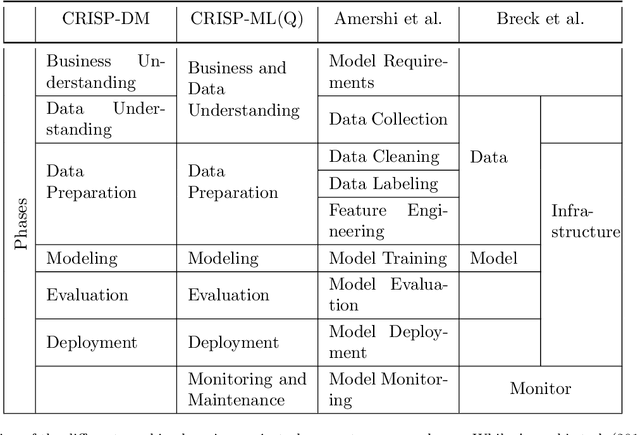
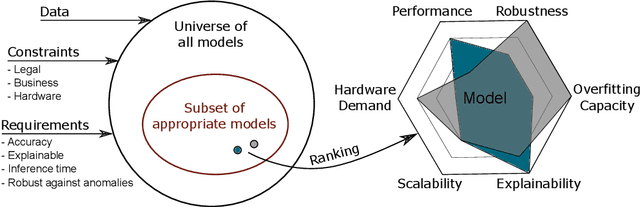
We propose a process model for the development of machine learning applications. It guides machine learning practitioners and project organizations from industry and academia with a checklist of tasks that spans the complete project life-cycle, ranging from the very first idea to the continuous maintenance of any machine learning application. With each task, we propose quality assurance methodology that is drawn from practical experience and scientific literature and that has proven to be general and stable enough to include them in best practices. We expand on CRISP-DM, a data mining process model that enjoys strong industry support but lacks to address machine learning specific tasks.

Local Bandwidth Estimation via Mixture of Gaussian Processes

Real world data often exhibit inhomogeneity - complexity of the target function, noise level, etc. are not uniform over the input space. We address the issue of estimating locally optimal kernel bandwidth as a way to describe inhomogeneity. Estimated kernel bandwidths can be used not only for improving the regression/classification performance, but also for Bayesian optimization and active learning, i.e., we need more samples in the region where the function complexity and the noise level are higher. Our method, called kernel mixture of kernel experts regression (KMKER) follows the concept of mixture of experts, which is constituted of several complementary inference models, the so called experts, where in advance a latent classifier, called the gate, predicts the best fitting expert for each test input to infer. For the experts we implement Gaussian process regression models at different (global) bandwidths and a multinomial kernel logistic regression model as the gate. The basic idea behind mixture of experts is, that several distinct ground truth functions over a joint input space drive the observations, which one may want to disentangle. Each expert is meant to model one of the incompatible functions such that each expert needs its individual set of hyperparameters. We differ from that idea in the sense that we assume only one ground truth function which however exhibits spacially inhomogeneous behavior. Under these assumptions we share the hyperparameters among the experts keeping their number constant. We compare KMKER to previous methods (which cope with inhomogeneity but do not provide the optimal bandwidth estimator) on artificial and benchmark data and analyze its performance and capability for interpretation on datasets from quantum chemistry. We also demonstrate how KMKER can be applied for automatic adaptive grid selection in fluid dynamics simulations.