Towards a Training Free Approach for 3D Scene Editing

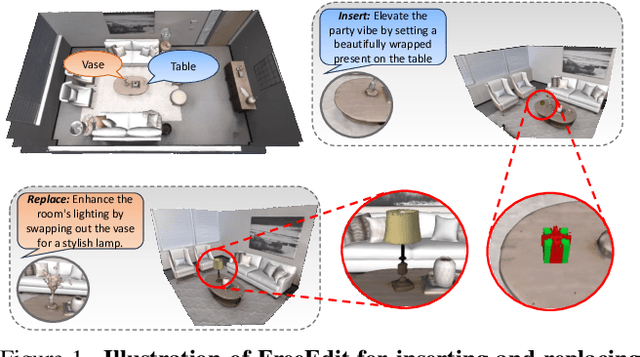
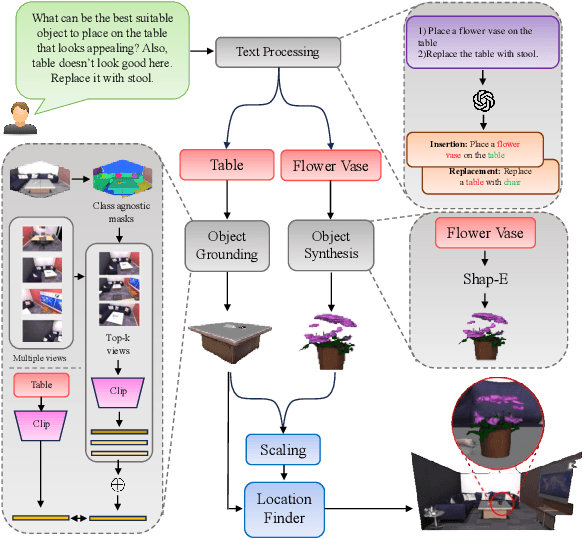
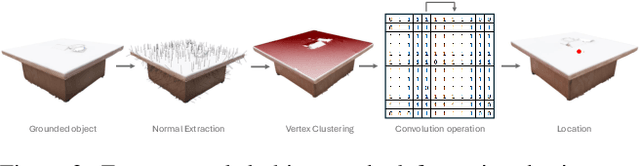
Text driven diffusion models have shown remarkable capabilities in editing images. However, when editing 3D scenes, existing works mostly rely on training a NeRF for 3D editing. Recent NeRF editing methods leverages edit operations by deploying 2D diffusion models and project these edits into 3D space. They require strong positional priors alongside text prompt to identify the edit location. These methods are operational on small 3D scenes and are more generalized to particular scene. They require training for each specific edit and cannot be exploited in real-time edits. To address these limitations, we propose a novel method, FreeEdit, to make edits in training free manner using mesh representations as a substitute for NeRF. Training-free methods are now a possibility because of the advances in foundation model's space. We leverage these models to bring a training-free alternative and introduce solutions for insertion, replacement and deletion. We consider insertion, replacement and deletion as basic blocks for performing intricate edits with certain combinations of these operations. Given a text prompt and a 3D scene, our model is capable of identifying what object should be inserted/replaced or deleted and location where edit should be performed. We also introduce a novel algorithm as part of FreeEdit to find the optimal location on grounding object for placement. We evaluate our model by comparing it with baseline models on a wide range of scenes using quantitative and qualitative metrics and showcase the merits of our method with respect to others.

Semantic Graph Consistency: Going Beyond Patches for Regularizing Self-Supervised Vision Transformers

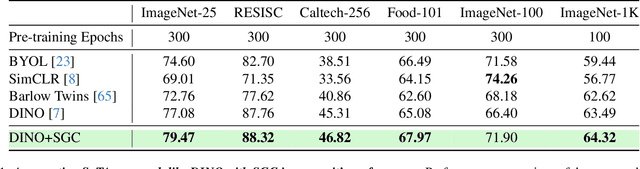
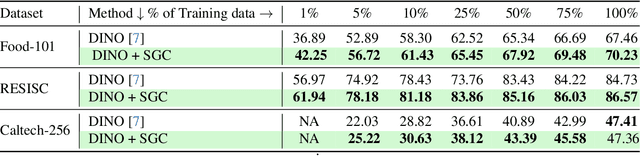
Self-supervised learning (SSL) with vision transformers (ViTs) has proven effective for representation learning as demonstrated by the impressive performance on various downstream tasks. Despite these successes, existing ViT-based SSL architectures do not fully exploit the ViT backbone, particularly the patch tokens of the ViT. In this paper, we introduce a novel Semantic Graph Consistency (SGC) module to regularize ViT-based SSL methods and leverage patch tokens effectively. We reconceptualize images as graphs, with image patches as nodes and infuse relational inductive biases by explicit message passing using Graph Neural Networks into the SSL framework. Our SGC loss acts as a regularizer, leveraging the underexploited patch tokens of ViTs to construct a graph and enforcing consistency between graph features across multiple views of an image. Extensive experiments on various datasets including ImageNet, RESISC and Food-101 show that our approach significantly improves the quality of learned representations, resulting in a 5-10\% increase in performance when limited labeled data is used for linear evaluation. These experiments coupled with a comprehensive set of ablations demonstrate the promise of our approach in various settings.

HOLMES: Hyper-Relational Knowledge Graphs for Multi-hop Question Answering using LLMs

Given unstructured text, Large Language Models (LLMs) are adept at answering simple (single-hop) questions. However, as the complexity of the questions increase, the performance of LLMs degrade. We believe this is due to the overhead associated with understanding the complex question followed by filtering and aggregating unstructured information in the raw text. Recent methods try to reduce this burden by integrating structured knowledge triples into the raw text, aiming to provide a structured overview that simplifies information processing. However, this simplistic approach is query-agnostic and the extracted facts are ambiguous as they lack context. To address these drawbacks and to enable LLMs to answer complex (multi-hop) questions with ease, we propose to use a knowledge graph (KG) that is context-aware and is distilled to contain query-relevant information. The use of our compressed distilled KG as input to the LLM results in our method utilizing up to $67\%$ fewer tokens to represent the query relevant information present in the supporting documents, compared to the state-of-the-art (SoTA) method. Our experiments show consistent improvements over the SoTA across several metrics (EM, F1, BERTScore, and Human Eval) on two popular benchmark datasets (HotpotQA and MuSiQue).

Synergizing Contrastive Learning and Optimal Transport for 3D Point Cloud Domain Adaptation

Recently, the fundamental problem of unsupervised domain adaptation (UDA) on 3D point clouds has been motivated by a wide variety of applications in robotics, virtual reality, and scene understanding, to name a few. The point cloud data acquisition procedures manifest themselves as significant domain discrepancies and geometric variations among both similar and dissimilar classes. The standard domain adaptation methods developed for images do not directly translate to point cloud data because of their complex geometric nature. To address this challenge, we leverage the idea of multimodality and alignment between distributions. We propose a new UDA architecture for point cloud classification that benefits from multimodal contrastive learning to get better class separation in both domains individually. Further, the use of optimal transport (OT) aims at learning source and target data distributions jointly to reduce the cross-domain shift and provide a better alignment. We conduct a comprehensive empirical study on PointDA-10 and GraspNetPC-10 and show that our method achieves state-of-the-art performance on GraspNetPC-10 (with approx 4-12% margin) and best average performance on PointDA-10. Our ablation studies and decision boundary analysis also validate the significance of our contrastive learning module and OT alignment.

BERTops: Studying BERT Representations under a Topological Lens

Proposing scoring functions to effectively understand, analyze and learn various properties of high dimensional hidden representations of large-scale transformer models like BERT can be a challenging task. In this work, we explore a new direction by studying the topological features of BERT hidden representations using persistent homology (PH). We propose a novel scoring function named "persistence scoring function (PSF)" which: (i) accurately captures the homology of the high-dimensional hidden representations and correlates well with the test set accuracy of a wide range of datasets and outperforms existing scoring metrics, (ii) captures interesting post fine-tuning "per-class" level properties from both qualitative and quantitative viewpoints, (iii) is more stable to perturbations as compared to the baseline functions, which makes it a very robust proxy, and (iv) finally, also serves as a predictor of the attack success rates for a wide category of black-box and white-box adversarial attack methods. Our extensive correlation experiments demonstrate the practical utility of PSF on various NLP tasks relevant to BERT.

ALLWAS: Active Learning on Language models in WASserstein space

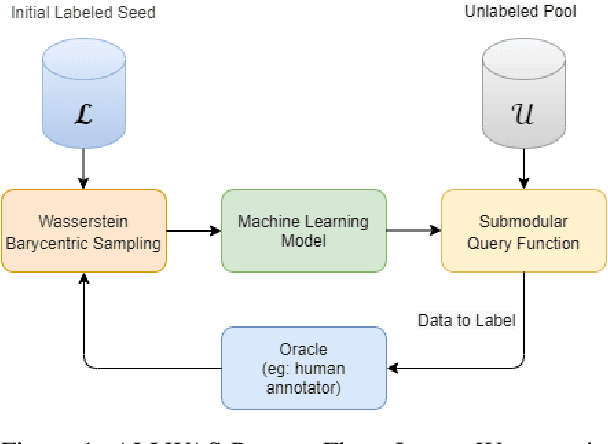
Active learning has emerged as a standard paradigm in areas with scarcity of labeled training data, such as in the medical domain. Language models have emerged as the prevalent choice of several natural language tasks due to the performance boost offered by these models. However, in several domains, such as medicine, the scarcity of labeled training data is a common issue. Also, these models may not work well in cases where class imbalance is prevalent. Active learning may prove helpful in these cases to boost the performance with a limited label budget. To this end, we propose a novel method using sampling techniques based on submodular optimization and optimal transport for active learning in language models, dubbed ALLWAS. We construct a sampling strategy based on submodular optimization of the designed objective in the gradient domain. Furthermore, to enable learning from few samples, we propose a novel strategy for sampling from the Wasserstein barycenters. Our empirical evaluations on standard benchmark datasets for text classification show that our methods perform significantly better (>20% relative increase in some cases) than existing approaches for active learning on language models.

Target Model Agnostic Adversarial Attacks with Query Budgets on Language Understanding Models

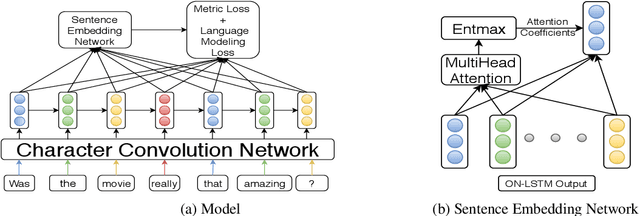
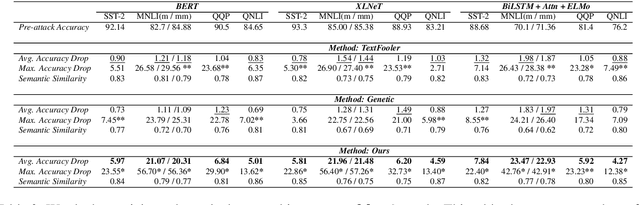
Despite significant improvements in natural language understanding models with the advent of models like BERT and XLNet, these neural-network based classifiers are vulnerable to blackbox adversarial attacks, where the attacker is only allowed to query the target model outputs. We add two more realistic restrictions on the attack methods, namely limiting the number of queries allowed (query budget) and crafting attacks that easily transfer across different pre-trained models (transferability), which render previous attack models impractical and ineffective. Here, we propose a target model agnostic adversarial attack method with a high degree of attack transferability across the attacked models. Our empirical studies show that in comparison to baseline methods, our method generates highly transferable adversarial sentences under the restriction of limited query budgets.

Understanding Higher-order Structures in Evolving Graphs: A Simplicial Complex based Kernel Estimation Approach

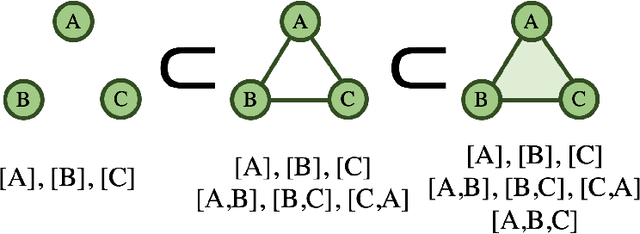
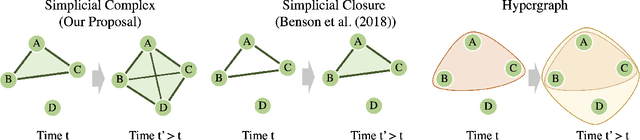
Dynamic graphs are rife with higher-order interactions, such as co-authorship relationships and protein-protein interactions in biological networks, that naturally arise between more than two nodes at once. In spite of the ubiquitous presence of such higher-order interactions, limited attention has been paid to the higher-order counterpart of the popular pairwise link prediction problem. Existing higher-order structure prediction methods are mostly based on heuristic feature extraction procedures, which work well in practice but lack theoretical guarantees. Such heuristics are primarily focused on predicting links in a static snapshot of the graph. Moreover, these heuristic-based methods fail to effectively utilize and benefit from the knowledge of latent substructures already present within the higher-order structures. In this paper, we overcome these obstacles by capturing higher-order interactions succinctly as \textit{simplices}, model their neighborhood by face-vectors, and develop a nonparametric kernel estimator for simplices that views the evolving graph from the perspective of a time process (i.e., a sequence of graph snapshots). Our method substantially outperforms several baseline higher-order prediction methods. As a theoretical achievement, we prove the consistency and asymptotic normality in terms of the Wasserstein distance of our estimator using Stein's method.

Self-Supervised Few-Shot Learning on Point Clouds

The increased availability of massive point clouds coupled with their utility in a wide variety of applications such as robotics, shape synthesis, and self-driving cars has attracted increased attention from both industry and academia. Recently, deep neural networks operating on labeled point clouds have shown promising results on supervised learning tasks like classification and segmentation. However, supervised learning leads to the cumbersome task of annotating the point clouds. To combat this problem, we propose two novel self-supervised pre-training tasks that encode a hierarchical partitioning of the point clouds using a cover-tree, where point cloud subsets lie within balls of varying radii at each level of the cover-tree. Furthermore, our self-supervised learning network is restricted to pre-train on the support set (comprising of scarce training examples) used to train the downstream network in a few-shot learning (FSL) setting. Finally, the fully-trained self-supervised network's point embeddings are input to the downstream task's network. We present a comprehensive empirical evaluation of our method on both downstream classification and segmentation tasks and show that supervised methods pre-trained with our self-supervised learning method significantly improve the accuracy of state-of-the-art methods. Additionally, our method also outperforms previous unsupervised methods in downstream classification tasks.

A Weighted Quiver Kernel using Functor Homology

In this paper, we propose a new homological method to study weighted directed networks. Our model of such networks is a directed graph $Q$ equipped with a weight function $w$ on the set $Q_{1}$ of arrows in $Q$. We require that the range $W$ of our weight function is equipped with an addition or a multiplication, i.e., $W$ is a monoid in the mathematical terminology. When $W$ is equipped with a representation on a vector space $M$, the standard method of homological algebra allows us to define the homology groups $H_{*}(Q,w;M)$. It is known that when $Q$ has no oriented cycles, $H_{n}(Q,w;M)=0$ for $n\ge 2$ and $H_{1}(Q,w;M)$ can be easily computed. This fact allows us to define a new graph kernel for weighted directed graphs. We made two sample computations with real data and found that our method is practically applicable.