Understanding Higher-order Structures in Evolving Graphs: A Simplicial Complex based Kernel Estimation Approach
Paper and Code
Feb 06, 2021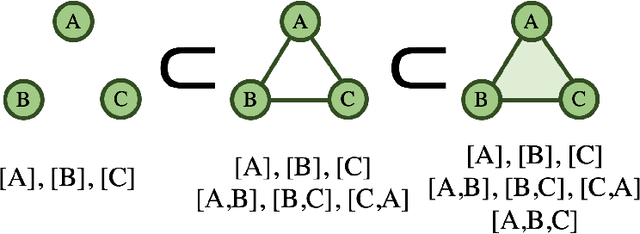

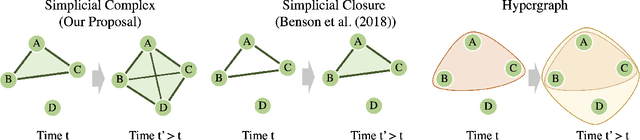

Dynamic graphs are rife with higher-order interactions, such as co-authorship relationships and protein-protein interactions in biological networks, that naturally arise between more than two nodes at once. In spite of the ubiquitous presence of such higher-order interactions, limited attention has been paid to the higher-order counterpart of the popular pairwise link prediction problem. Existing higher-order structure prediction methods are mostly based on heuristic feature extraction procedures, which work well in practice but lack theoretical guarantees. Such heuristics are primarily focused on predicting links in a static snapshot of the graph. Moreover, these heuristic-based methods fail to effectively utilize and benefit from the knowledge of latent substructures already present within the higher-order structures. In this paper, we overcome these obstacles by capturing higher-order interactions succinctly as \textit{simplices}, model their neighborhood by face-vectors, and develop a nonparametric kernel estimator for simplices that views the evolving graph from the perspective of a time process (i.e., a sequence of graph snapshots). Our method substantially outperforms several baseline higher-order prediction methods. As a theoretical achievement, we prove the consistency and asymptotic normality in terms of the Wasserstein distance of our estimator using Stein's method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge