The Degrees of Freedom of Partial Least Squares Regression

The derivation of statistical properties for Partial Least Squares regression can be a challenging task. The reason is that the construction of latent components from the predictor variables also depends on the response variable. While this typically leads to good performance and interpretable models in practice, it makes the statistical analysis more involved. In this work, we study the intrinsic complexity of Partial Least Squares Regression. Our contribution is an unbiased estimate of its Degrees of Freedom. It is defined as the trace of the first derivative of the fitted values, seen as a function of the response. We establish two equivalent representations that rely on the close connection of Partial Least Squares to matrix decompositions and Krylov subspace techniques. We show that the Degrees of Freedom depend on the collinearity of the predictor variables: The lower the collinearity is, the higher the Degrees of Freedom are. In particular, they are typically higher than the naive approach that defines the Degrees of Freedom as the number of components. Further, we illustrate how the Degrees of Freedom approach can be used for the comparison of different regression methods. In the experimental section, we show that our Degrees of Freedom estimate in combination with information criteria is useful for model selection.

Optimal learning rates for Kernel Conjugate Gradient regression

We prove rates of convergence in the statistical sense for kernel-based least squares regression using a conjugate gradient algorithm, where regularization against overfitting is obtained by early stopping. This method is directly related to Kernel Partial Least Squares, a regression method that combines supervised dimensionality reduction with least squares projection. The rates depend on two key quantities: first, on the regularity of the target regression function and second, on the intrinsic dimensionality of the data mapped into the kernel space. Lower bounds on attainable rates depending on these two quantities were established in earlier literature, and we obtain upper bounds for the considered method that match these lower bounds (up to a log factor) if the true regression function belongs to the reproducing kernel Hilbert space. If this assumption is not fulfilled, we obtain similar convergence rates provided additional unlabeled data are available. The order of the learning rates match state-of-the-art results that were recently obtained for least squares support vector machines and for linear regularization operators.

Kernel Partial Least Squares is Universally Consistent

We prove the statistical consistency of kernel Partial Least Squares Regression applied to a bounded regression learning problem on a reproducing kernel Hilbert space. Partial Least Squares stands out of well-known classical approaches as e.g. Ridge Regression or Principal Components Regression, as it is not defined as the solution of a global cost minimization procedure over a fixed model nor is it a linear estimator. Instead, approximate solutions are constructed by projections onto a nested set of data-dependent subspaces. To prove consistency, we exploit the known fact that Partial Least Squares is equivalent to the conjugate gradient algorithm in combination with early stopping. The choice of the stopping rule (number of iterations) is a crucial point. We study two empirical stopping rules. The first one monitors the estimation error in each iteration step of Partial Least Squares, and the second one estimates the empirical complexity in terms of a condition number. Both stopping rules lead to universally consistent estimators provided the kernel is universal.

The Feature Importance Ranking Measure

Most accurate predictions are typically obtained by learning machines with complex feature spaces (as e.g. induced by kernels). Unfortunately, such decision rules are hardly accessible to humans and cannot easily be used to gain insights about the application domain. Therefore, one often resorts to linear models in combination with variable selection, thereby sacrificing some predictive power for presumptive interpretability. Here, we introduce the Feature Importance Ranking Measure (FIRM), which by retrospective analysis of arbitrary learning machines allows to achieve both excellent predictive performance and superior interpretation. In contrast to standard raw feature weighting, FIRM takes the underlying correlation structure of the features into account. Thereby, it is able to discover the most relevant features, even if their appearance in the training data is entirely prevented by noise. The desirable properties of FIRM are investigated analytically and illustrated in simulations.

Lanczos Approximations for the Speedup of Kernel Partial Least Squares Regression

The runtime for Kernel Partial Least Squares (KPLS) to compute the fit is quadratic in the number of examples. However, the necessity of obtaining sensitivity measures as degrees of freedom for model selection or confidence intervals for more detailed analysis requires cubic runtime, and thus constitutes a computational bottleneck in real-world data analysis. We propose a novel algorithm for KPLS which not only computes (a) the fit, but also (b) its approximate degrees of freedom and (c) error bars in quadratic runtime. The algorithm exploits a close connection between Kernel PLS and the Lanczos algorithm for approximating the eigenvalues of symmetric matrices, and uses this approximation to compute the trace of powers of the kernel matrix in quadratic runtime.

Sparse Causal Discovery in Multivariate Time Series

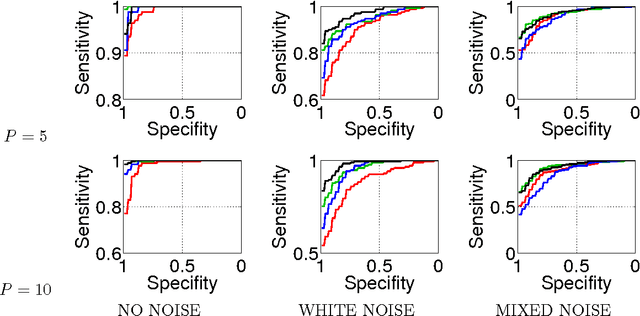
Our goal is to estimate causal interactions in multivariate time series. Using vector autoregressive (VAR) models, these can be defined based on non-vanishing coefficients belonging to respective time-lagged instances. As in most cases a parsimonious causality structure is assumed, a promising approach to causal discovery consists in fitting VAR models with an additional sparsity-promoting regularization. Along this line we here propose that sparsity should be enforced for the subgroups of coefficients that belong to each pair of time series, as the absence of a causal relation requires the coefficients for all time-lags to become jointly zero. Such behavior can be achieved by means of l1-l2-norm regularized regression, for which an efficient active set solver has been proposed recently. Our method is shown to outperform standard methods in recovering simulated causality graphs. The results are on par with a second novel approach which uses multiple statistical testing.