Modeling sparse connectivity between underlying brain sources for EEG/MEG

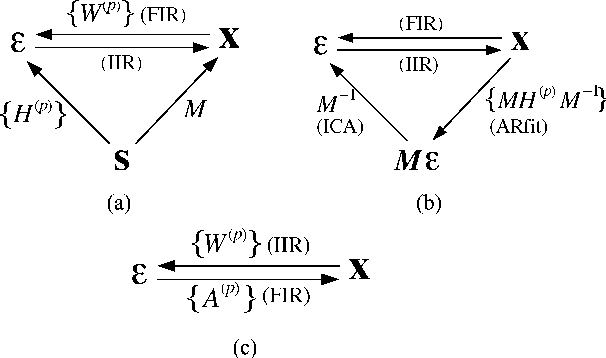
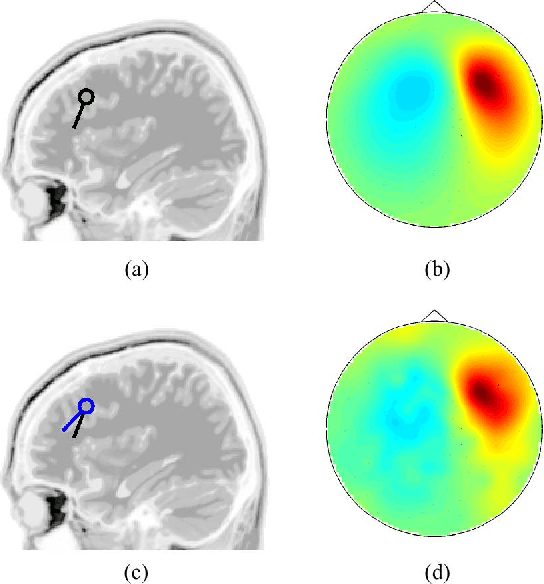
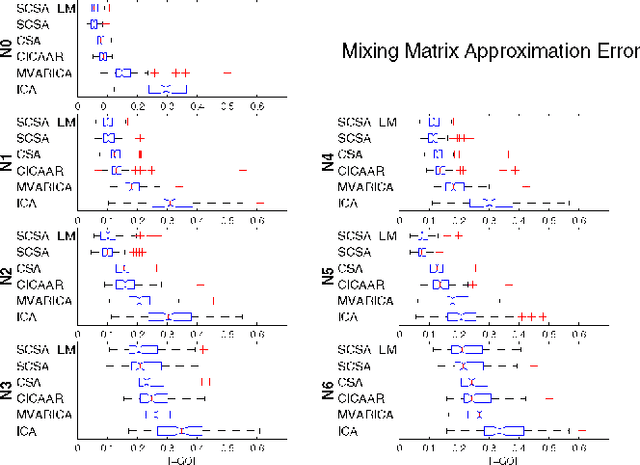
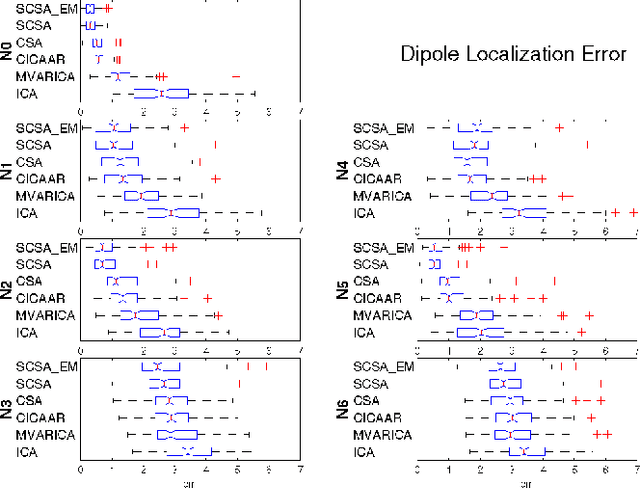
We propose a novel technique to assess functional brain connectivity in EEG/MEG signals. Our method, called Sparsely-Connected Sources Analysis (SCSA), can overcome the problem of volume conduction by modeling neural data innovatively with the following ingredients: (a) the EEG is assumed to be a linear mixture of correlated sources following a multivariate autoregressive (MVAR) model, (b) the demixing is estimated jointly with the source MVAR parameters, (c) overfitting is avoided by using the Group Lasso penalty. This approach allows to extract the appropriate level cross-talk between the extracted sources and in this manner we obtain a sparse data-driven model of functional connectivity. We demonstrate the usefulness of SCSA with simulated data, and compare to a number of existing algorithms with excellent results.

Sparse Causal Discovery in Multivariate Time Series

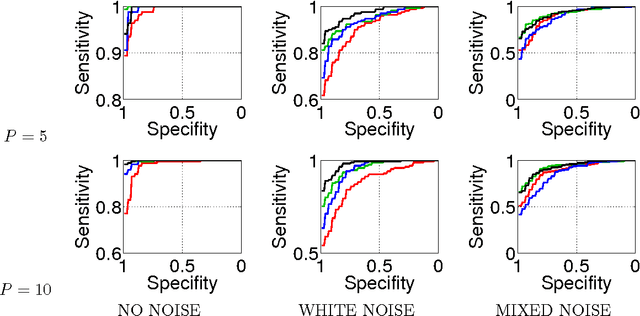
Our goal is to estimate causal interactions in multivariate time series. Using vector autoregressive (VAR) models, these can be defined based on non-vanishing coefficients belonging to respective time-lagged instances. As in most cases a parsimonious causality structure is assumed, a promising approach to causal discovery consists in fitting VAR models with an additional sparsity-promoting regularization. Along this line we here propose that sparsity should be enforced for the subgroups of coefficients that belong to each pair of time series, as the absence of a causal relation requires the coefficients for all time-lags to become jointly zero. Such behavior can be achieved by means of l1-l2-norm regularized regression, for which an efficient active set solver has been proposed recently. Our method is shown to outperform standard methods in recovering simulated causality graphs. The results are on par with a second novel approach which uses multiple statistical testing.