Path-Gradient Estimators for Continuous Normalizing Flows
Paper and Code
Jun 17, 2022

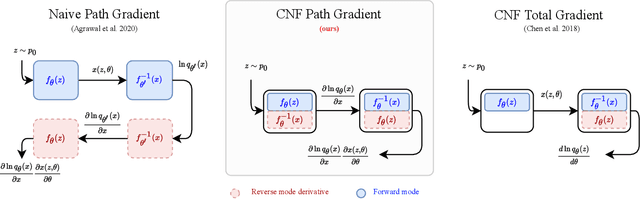

Recent work has established a path-gradient estimator for simple variational Gaussian distributions and has argued that the path-gradient is particularly beneficial in the regime in which the variational distribution approaches the exact target distribution. In many applications, this regime can however not be reached by a simple Gaussian variational distribution. In this work, we overcome this crucial limitation by proposing a path-gradient estimator for the considerably more expressive variational family of continuous normalizing flows. We outline an efficient algorithm to calculate this estimator and establish its superior performance empirically.
* 8 pages, 5 figures, 39th International Conference on Machine Learning
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge