Elia Cellini
A scalable flow-based approach to mitigate topological freezing
Jan 28, 2026Abstract:As lattice gauge theories with non-trivial topological features are driven towards the continuum limit, standard Markov Chain Monte Carlo simulations suffer for topological freezing, i.e., a dramatic growth of autocorrelations in topological observables. A widely used strategy is the adoption of Open Boundary Conditions (OBC), which restores ergodic sampling of topology but at the price of breaking translation invariance and introducing unphysical boundary artifacts. In this contribution we summarize a scalable, exact flow-based strategy to remove them by transporting configurations from a prior with a OBC defect to a fully periodic ensemble, and apply it to 4d SU(3) Yang--Mills theory. The method is based on a Stochastic Normalizing Flow (SNF) that alternates non-equilibrium Monte Carlo updates with localized, gauge-equivariant defect coupling layers implemented via masked parametric stout smearing. Training is performed by minimizing the average dissipated work, equivalent to a Kullback--Leibler divergence between forward and reverse non-equilibrium path measures, to achieve more reversible trajectories and improved efficiency. We discuss the scaling with the number of degrees of freedom affected by the defect and show that defect SNFs achieve better performances than purely stochastic non-equilibrium methods at comparable cost. Finally, we validate the approach by reproducing reference results for the topological susceptibility.
Scaling flow-based approaches for topology sampling in $\mathrm{SU}(3)$ gauge theory
Oct 29, 2025Abstract:We develop a methodology based on out-of-equilibrium simulations to mitigate topological freezing when approaching the continuum limit of lattice gauge theories. We reduce the autocorrelation of the topological charge employing open boundary conditions, while removing exactly their unphysical effects using a non-equilibrium Monte Carlo approach in which periodic boundary conditions are gradually switched on. We perform a detailed analysis of the computational costs of this strategy in the case of the four-dimensional $\mathrm{SU}(3)$ Yang-Mills theory. After achieving full control of the scaling, we outline a clear strategy to sample topology efficiently in the continuum limit, which we check at lattice spacings as small as $0.045$ fm. We also generalize this approach by designing a customized Stochastic Normalizing Flow for evolutions in the boundary conditions, obtaining superior performances with respect to the purely stochastic non-equilibrium approach, and paving the way for more efficient future flow-based solutions.
Multilevel Generative Samplers for Investigating Critical Phenomena
Mar 13, 2025Abstract:Investigating critical phenomena or phase transitions is of high interest in physics and chemistry, for which Monte Carlo (MC) simulations, a crucial tool for numerically analyzing macroscopic properties of given systems, are often hindered by an emerging divergence of correlation length -- known as scale invariance at criticality (SIC) in the renormalization group theory. SIC causes the system to behave the same at any length scale, from which many existing sampling methods suffer: long-range correlations cause critical slowing down in Markov chain Monte Carlo (MCMC), and require intractably large receptive fields for generative samplers. In this paper, we propose a Renormalization-informed Generative Critical Sampler (RiGCS) -- a novel sampler specialized for near-critical systems, where SIC is leveraged as an advantage rather than a nuisance. Specifically, RiGCS builds on MultiLevel Monte Carlo (MLMC) with Heat Bath (HB) algorithms, which perform ancestral sampling from low-resolution to high-resolution lattice configurations with site-wise-independent conditional HB sampling. Although MLMC-HB is highly efficient under exact SIC, it suffers from a low acceptance rate under slight SIC violation. Notably, SIC violation always occurs in finite-size systems, and may induce long-range and higher-order interactions in the renormalized distributions, which are not considered by independent HB samplers. RiGCS enhances MLMC-HB by replacing a part of the conditional HB sampler with generative models that capture those residual interactions and improve the sampling efficiency. Our experiments show that the effective sample size of RiGCS is a few orders of magnitude higher than state-of-the-art generative model baselines in sampling configurations for 128x128 two-dimensional Ising systems.
Stochastic normalizing flows for Effective String Theory
Dec 26, 2024Abstract:Effective String Theory (EST) is a powerful tool used to study confinement in pure gauge theories by modeling the confining flux tube connecting a static quark-anti-quark pair as a thin vibrating string. Recently, flow-based samplers have been applied as an efficient numerical method to study EST regularized on the lattice, opening the route to study observables previously inaccessible to standard analytical methods. Flow-based samplers are a class of algorithms based on Normalizing Flows (NFs), deep generative models recently proposed as a promising alternative to traditional Markov Chain Monte Carlo methods in lattice field theory calculations. By combining NF layers with out-of-equilibrium stochastic updates, we obtain Stochastic Normalizing Flows (SNFs), a scalable class of machine learning algorithms that can be explained in terms of stochastic thermodynamics. In this contribution, we outline EST and SNFs, and report some numerical results for the shape of the flux tube.
Scaling of Stochastic Normalizing Flows in $\mathrm{SU}(3)$ lattice gauge theory
Nov 29, 2024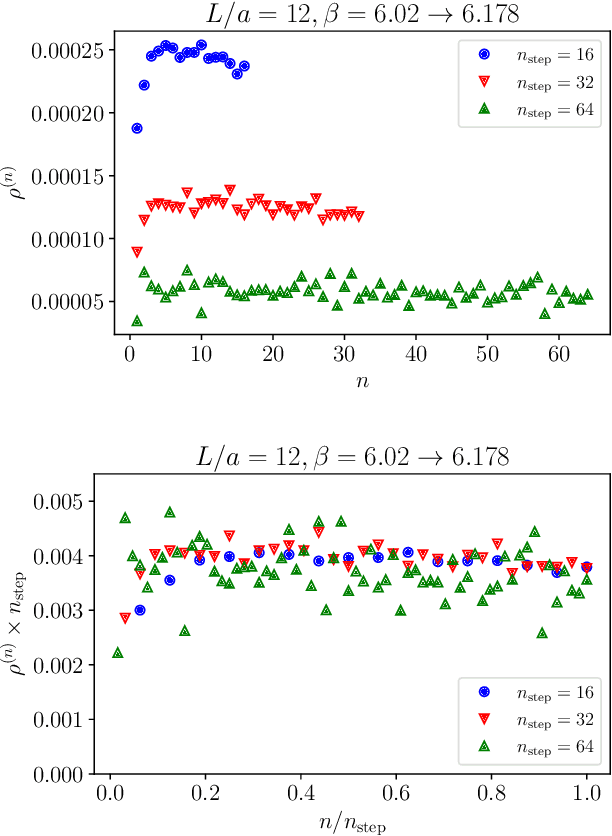
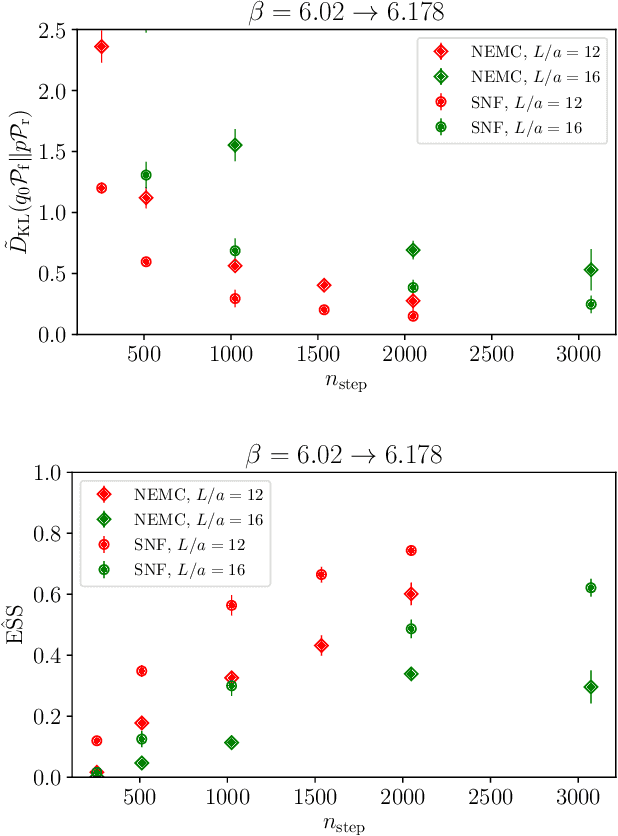
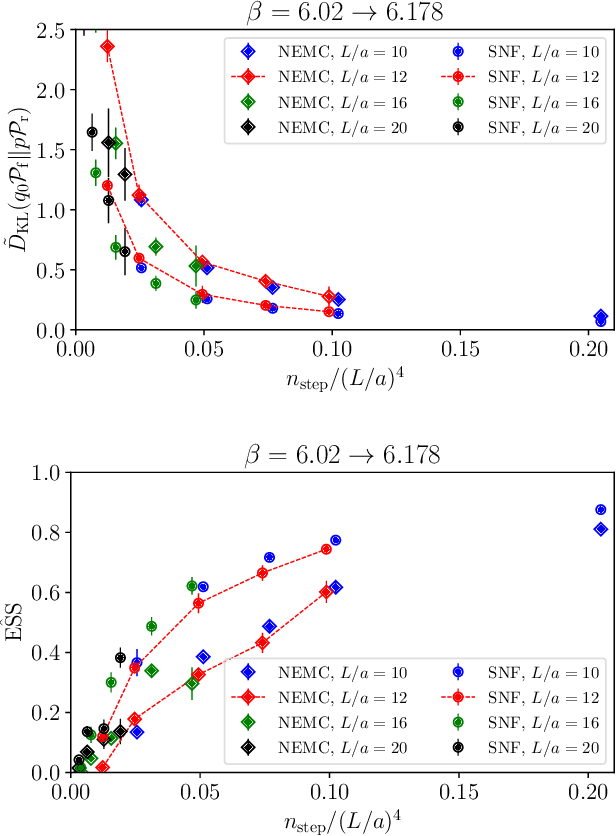
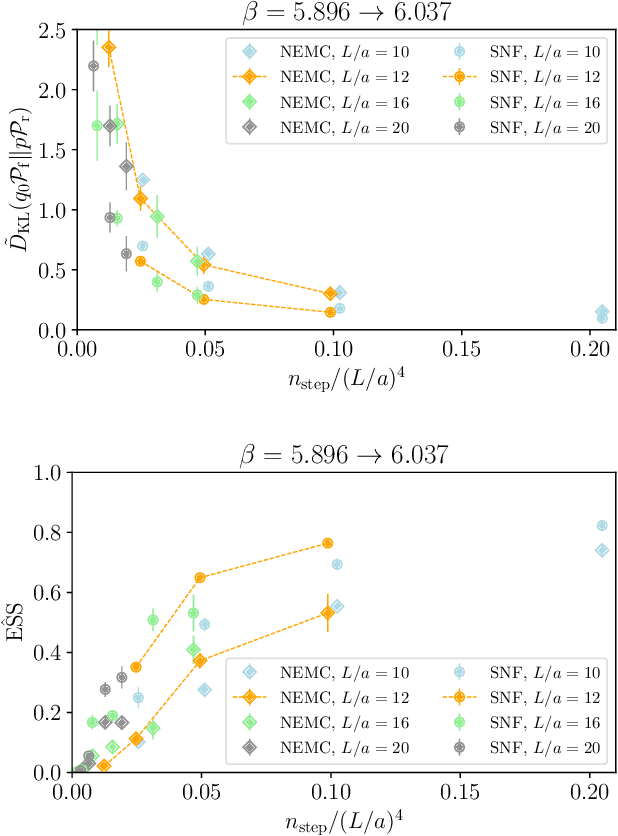
Abstract:Non-equilibrium Markov Chain Monte Carlo (NE-MCMC) simulations provide a well-understood framework based on Jarzynski's equality to sample from a target probability distribution. By driving a base probability distribution out of equilibrium, observables are computed without the need to thermalize. If the base distribution is characterized by mild autocorrelations, this approach provides a way to mitigate critical slowing down. Out-of-equilibrium evolutions share the same framework of flow-based approaches and they can be naturally combined into a novel architecture called Stochastic Normalizing Flows (SNFs). In this work we present the first implementation of SNFs for $\mathrm{SU}(3)$ lattice gauge theory in 4 dimensions, defined by introducing gauge-equivariant layers between out-of-equilibrium Monte Carlo updates. The core of our analysis is focused on the promising scaling properties of this architecture with the degrees of freedom of the system, which are directly inherited from NE-MCMC. Finally, we discuss how systematic improvements of this approach can realistically lead to a general and yet efficient sampling strategy at fine lattice spacings for observables affected by long autocorrelation times.
Flow-based Sampling for Entanglement Entropy and the Machine Learning of Defects
Oct 18, 2024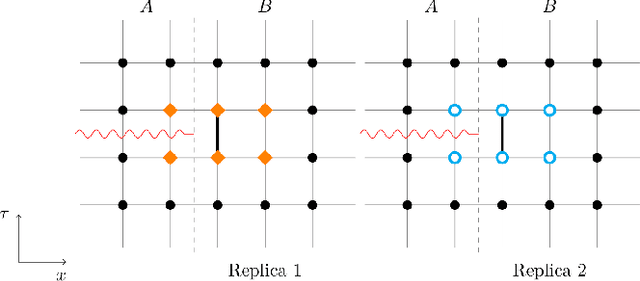
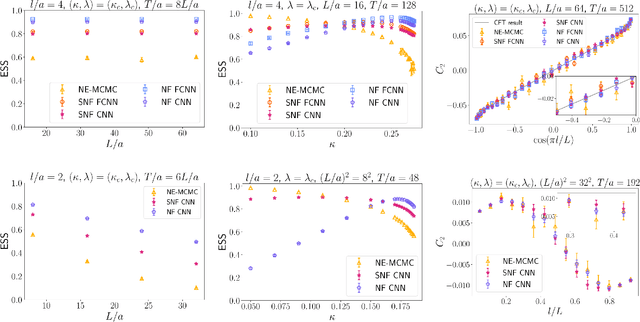
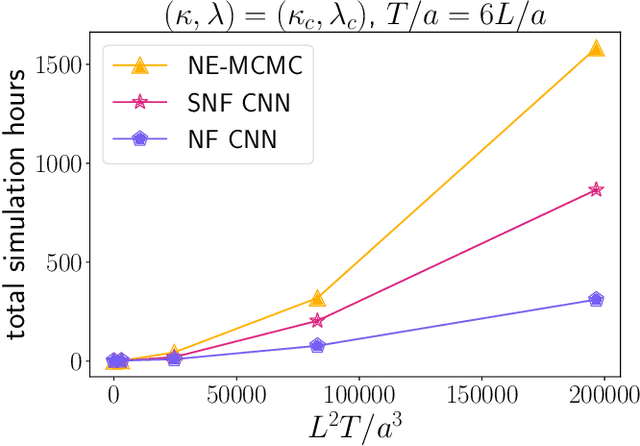
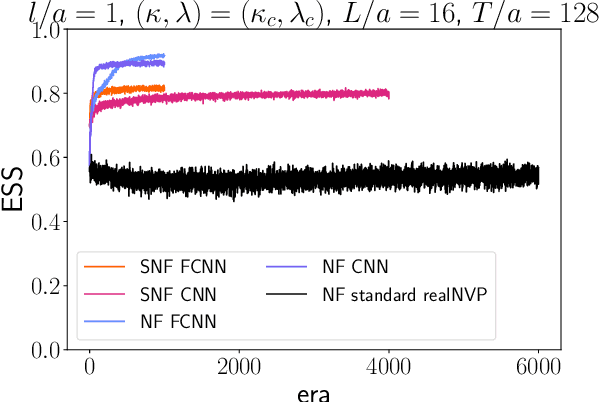
Abstract:We introduce a novel technique to numerically calculate R\'enyi entanglement entropies in lattice quantum field theory using generative models. We describe how flow-based approaches can be combined with the replica trick using a custom neural-network architecture around a lattice defect connecting two replicas. Numerical tests for the $\phi^4$ scalar field theory in two and three dimensions demonstrate that our technique outperforms state-of-the-art Monte Carlo calculations, and exhibit a promising scaling with the defect size.
Numerical determination of the width and shape of the effective string using Stochastic Normalizing Flows
Sep 24, 2024Abstract:Flow-based architectures have recently proved to be an efficient tool for numerical simulations of Effective String Theories regularized on the lattice that otherwise cannot be efficiently sampled by standard Monte Carlo methods. In this work we use Stochastic Normalizing Flows, a state-of-the-art deep-learning architecture based on non-equilibrium Monte Carlo simulations, to study different effective string models. After testing the reliability of this approach through a comparison with exact results for the Nambu-Got\={o} model, we discuss results on observables that are challenging to study analytically, such as the width of the string and the shape of the flux density. Furthermore, we perform a novel numerical study of Effective String Theories with terms beyond the Nambu-Got\={o} action, including a broader discussion on their significance for lattice gauge theories. These results establish the reliability and feasibility of flow-based samplers for Effective String Theories and pave the way for future applications on more complex models.
Sampling the lattice Nambu-Goto string using Continuous Normalizing Flows
Jul 03, 2023Abstract:Effective String Theory (EST) represents a powerful non-perturbative approach to describe confinement in Yang-Mills theory that models the confining flux tube as a thin vibrating string. EST calculations are usually performed using the zeta-function regularization: however there are situations (for instance the study of the shape of the flux tube or of the higher order corrections beyond the Nambu-Goto EST) which involve observables that are too complex to be addressed in this way. In this paper we propose a numerical approach based on recent advances in machine learning methods to circumvent this problem. Using as a laboratory the Nambu-Goto string, we show that by using a new class of deep generative models called Continuous Normalizing Flows it is possible to obtain reliable numerical estimates of EST predictions.
Stochastic normalizing flows as non-equilibrium transformations
Jan 21, 2022



Abstract:Normalizing flows are a class of deep generative models that provide a promising route to sample lattice field theories more efficiently than conventional Monte~Carlo simulations. In this work we show that the theoretical framework of stochastic normalizing flows, in which neural-network layers are combined with Monte~Carlo updates, is the same that underlies out-of-equilibrium simulations based on Jarzynski's equality, which have been recently deployed to compute free-energy differences in lattice gauge theories. We lay out a strategy to optimize the efficiency of this extended class of generative models and present examples of applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge