Reinforcement Learning Based Prediction of PID Controller Gains for Quadrotor UAVs

A reinforcement learning (RL) based methodology is proposed and implemented for online fine-tuning of PID controller gains, thus, improving quadrotor effective and accurate trajectory tracking. The RL agent is first trained offline on a quadrotor PID attitude controller and then validated through simulations and experimental flights. RL exploits a Deep Deterministic Policy Gradient (DDPG) algorithm, which is an off-policy actor-critic method. Training and simulation studies are performed using Matlab/Simulink and the UAV Toolbox Support Package for PX4 Autopilots. Performance evaluation and comparison studies are performed between the hand-tuned and RL-based tuned approaches. The results show that the controller parameters based on RL are adjusted during flights, achieving the smallest attitude errors, thus significantly improving attitude tracking performance compared to the hand-tuned approach.

Benchmarking Quantum Convolutional Neural Networks for Signal Classification in Simulated Gamma-Ray Burst Detection

This study evaluates the use of Quantum Convolutional Neural Networks (QCNNs) for identifying signals resembling Gamma-Ray Bursts (GRBs) within simulated astrophysical datasets in the form of light curves. The task addressed here focuses on distinguishing GRB-like signals from background noise in simulated Cherenkov Telescope Array Observatory (CTAO) data, the next-generation astrophysical observatory for very high-energy gamma-ray science. QCNNs, a quantum counterpart of classical Convolutional Neural Networks (CNNs), leverage quantum principles to process and analyze high-dimensional data efficiently. We implemented a hybrid quantum-classical machine learning technique using the Qiskit framework, with the QCNNs trained on a quantum simulator. Several QCNN architectures were tested, employing different encoding methods such as Data Reuploading and Amplitude encoding. Key findings include that QCNNs achieved accuracy comparable to classical CNNs, often surpassing 90\%, while using fewer parameters, potentially leading to more efficient models in terms of computational resources. A benchmark study further examined how hyperparameters like the number of qubits and encoding methods affected performance, with more qubits and advanced encoding methods generally enhancing accuracy but increasing complexity. QCNNs showed robust performance on time-series datasets, successfully detecting GRB signals with high precision. The research is a pioneering effort in applying QCNNs to astrophysics, offering insights into their potential and limitations. This work sets the stage for future investigations to fully realize the advantages of QCNNs in astrophysical data analysis.

Game-theoretical trajectory planning enhances social acceptability for humans

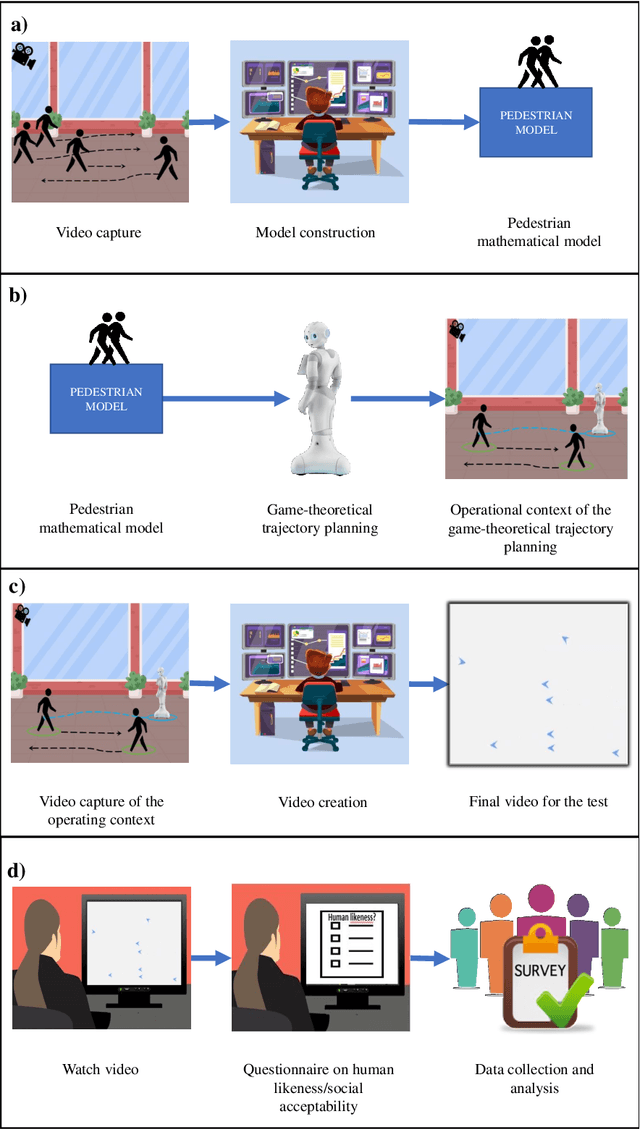
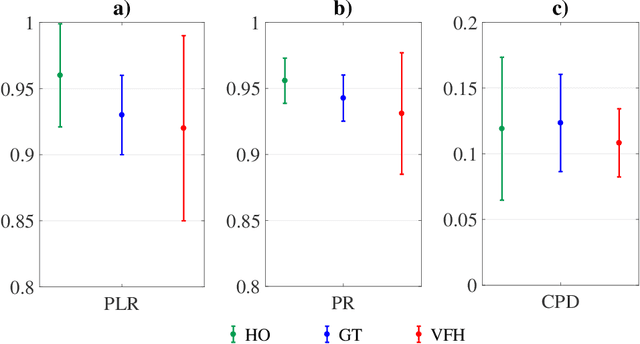
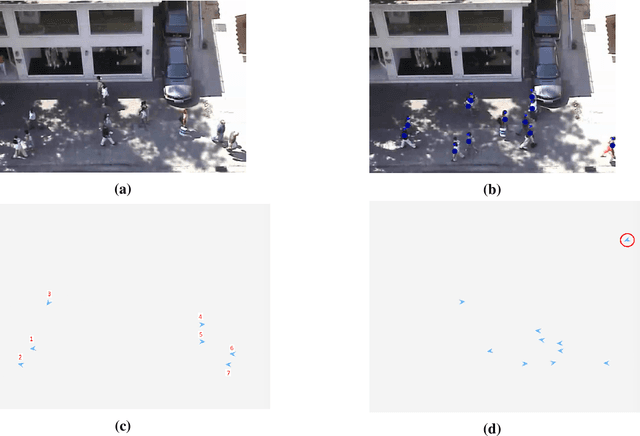
Since humans and robots are increasingly sharing portions of their operational spaces, experimental evidence is needed to ascertain the safety and social acceptability of robots in human-populated environments. Although several studies have aimed at devising strategies for robot trajectory planning to perform \emph{safe} motion in populated environments, a few efforts have \emph{measured} to what extent a robot trajectory is \emph{accepted} by humans. Here, we present a navigation system for autonomous robotics that ensures safety and social acceptability of robotic trajectories. We overcome the typical reactive nature of state-of-the-art trajectory planners by leveraging non-cooperative game theory to design a planner that encapsulates human-like features of preservation of a vital space, recognition of groups, sequential and strategized decision making, and smooth obstacle avoidance. Social acceptability is measured through a variation of the Turing test administered in the form of a survey questionnaire to a pool of 691 participants. Comparison terms for our tests are a state-of-the-art navigation algorithm (Enhanced Vector Field Histogram, VFH) and purely human trajectories. While all participants easily recognized the non-human nature of VFH-generated trajectories, the distinction between game-theoretical trajectories and human ones were hardly revealed. These results mark a strong milestone toward the full integration of robots in social environments.

Reachability analysis in stochastic directed graphs by reinforcement learning

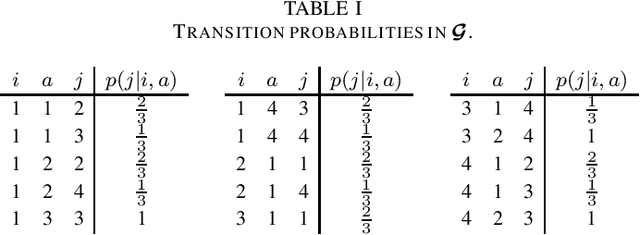
We characterize the reachability probabilities in stochastic directed graphs by means of reinforcement learning methods. In particular, we show that the dynamics of the transition probabilities in a stochastic digraph can be modeled via a difference inclusion, which, in turn, can be interpreted as a Markov decision process. Using the latter framework, we offer a methodology to design reward functions to provide upper and lower bounds on the reachability probabilities of a set of nodes for stochastic digraphs. The effectiveness of the proposed technique is demonstrated by application to the diffusion of epidemic diseases over time-varying contact networks generated by the proximity patterns of mobile agents.

Distributed Estimation of State and Parameters in Multi-Agent Cooperative Load Manipulation

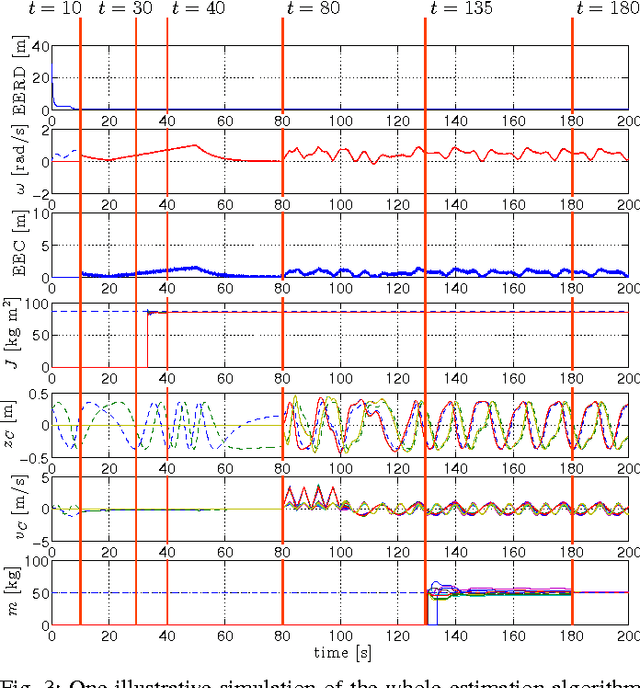
We present two distributed methods for the estimation of the kinematic parameters, the dynamic parameters, and the kinematic state of an unknown planar body manipulated by a decentralized multi-agent system. The proposed approaches rely on the rigid body kinematics and dynamics, on nonlinear observation theory, and on consensus algorithms. The only three requirements are that each agent can exert a 2D wrench on the load, it can measure the velocity of its contact point, and that the communication graph is connected. Both theoretical nonlinear observability analysis and convergence proofs are provided. The first method assumes constant parameters while the second one can deal with time-varying parameters and can be applied in parallel to any task-oriented control law. For the cases in which a control law is not provided, we propose a distributed and safe control strategy satisfying the observability condition. The effectiveness and robustness of the estimation strategy is showcased by means of realistic MonteCarlo simulations.