Parallel Branch Model Predictive Control on GPUs

We present a parallel GPU-accelerated solver for branch Model Predictive Control problems. Based on iterative LQR methods, our solver exploits the tree-sparse structure and implements temporal parallelism using the parallel scan algorithm. Consequently, the proposed solver enables parallelism across both the prediction horizon and the scenarios. In addition, we utilize an augmented Lagrangian method to handle general inequality constraints. We compare our solver with state-of-the-art numerical solvers in two automated driving applications. The numerical results demonstrate that, compared to CPU-based solvers, our solver achieves competitive performance for problems with short horizons and small-scale trees, while outperforming other solvers on large-scale problems.

Estimation Network Design framework for efficient distributed optimization

Distributed decision problems features a group of agents that can only communicate over a peer-to-peer network, without a central memory. In applications such as network control and data ranking, each agent is only affected by a small portion of the decision vector: this sparsity is typically ignored in distributed algorithms, while it could be leveraged to improve efficiency and scalability. To address this issue, our recent paper introduces Estimation Network Design (END), a graph theoretical language for the analysis and design of distributed iterations. END algorithms can be tuned to exploit the sparsity of specific problem instances, reducing communication overhead and minimizing redundancy, yet without requiring case-by-case convergence analysis. In this paper, we showcase the flexility of END in the context of distributed optimization. In particular, we study the sparsity-aware version of many established methods, including ADMM, AugDGM and Push-Sum DGD. Simulations on an estimation problem in sensor networks demonstrate that END algorithms can boost convergence speed and greatly reduce the communication and memory cost.

An Efficient Risk-aware Branch MPC for Automated Driving that is Robust to Uncertain Vehicle Behaviors

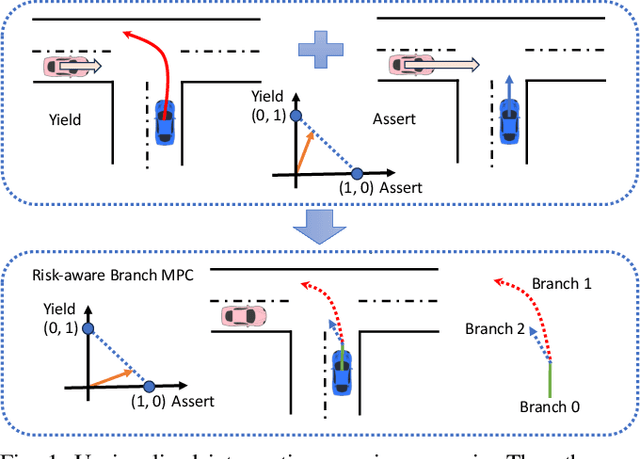
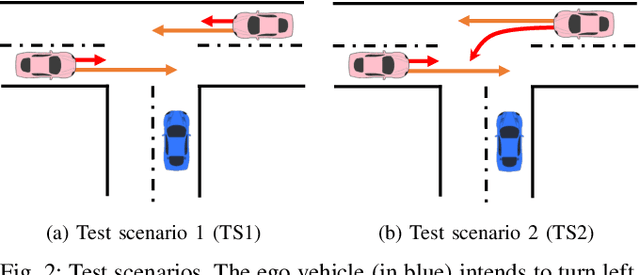
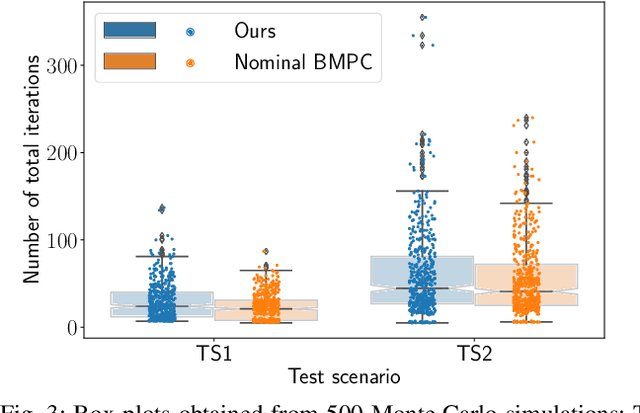
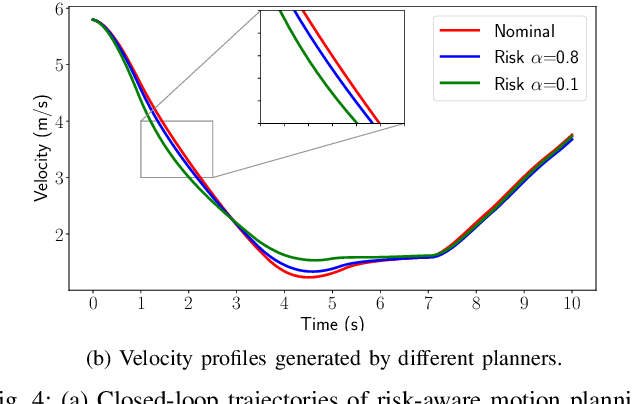
One of the critical challenges in automated driving is ensuring safety of automated vehicles despite the unknown behavior of the other vehicles. Although motion prediction modules are able to generate a probability distribution associated with various behavior modes, their probabilistic estimates are often inaccurate, thus leading to a possibly unsafe trajectory. To overcome this challenge, we propose a risk-aware motion planning framework that appropriately accounts for the ambiguity in the estimated probability distribution. We formulate the risk-aware motion planning problem as a min-max optimization problem and develop an efficient iterative method by incorporating a regularization term in the probability update step. Via extensive numerical studies, we validate the convergence of our method and demonstrate its advantages compared to the state-of-the-art approaches.

An Efficient Game-Theoretic Planner for Automated Lane Merging with Multi-Modal Behavior Understanding

In this paper, we propose a novel behavior planner that combines game theory with search-based planning for automated lane merging. Specifically, inspired by human drivers, we model the interaction between vehicles as a gap selection process. To overcome the challenge of multi-modal behavior exhibited by the surrounding vehicles, we formulate the trajectory selection as a matrix game and compute an equilibrium. Next, we validate our proposed planner in the high-fidelity simulator CARLA and demonstrate its effectiveness in handling interactions in dense traffic scenarios.

Game-theoretical trajectory planning enhances social acceptability for humans

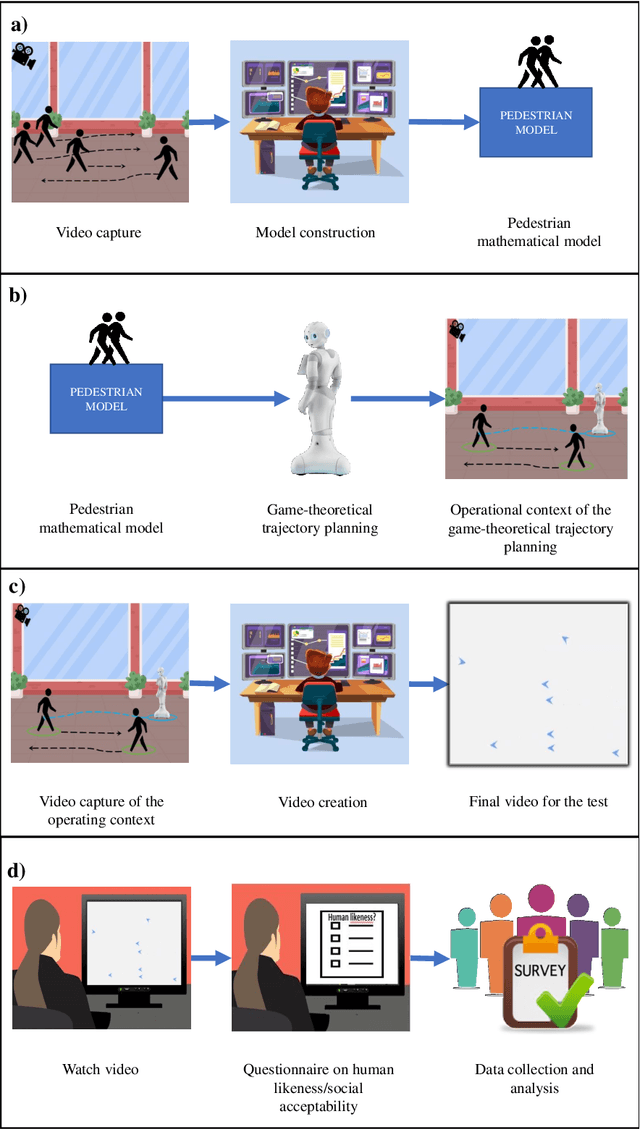
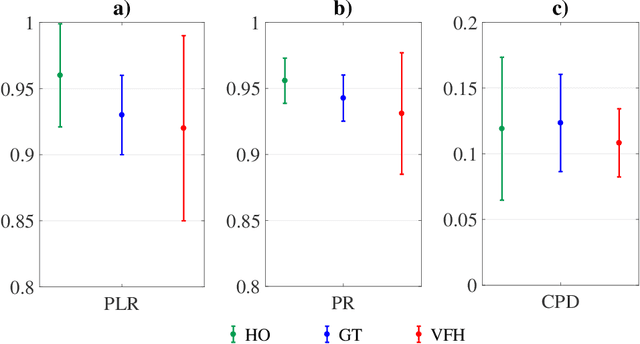
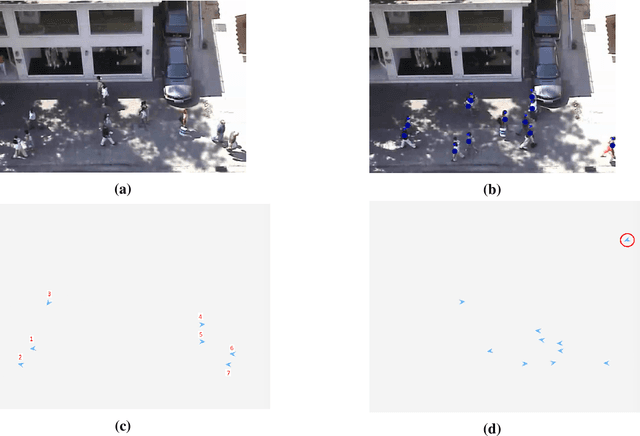
Since humans and robots are increasingly sharing portions of their operational spaces, experimental evidence is needed to ascertain the safety and social acceptability of robots in human-populated environments. Although several studies have aimed at devising strategies for robot trajectory planning to perform \emph{safe} motion in populated environments, a few efforts have \emph{measured} to what extent a robot trajectory is \emph{accepted} by humans. Here, we present a navigation system for autonomous robotics that ensures safety and social acceptability of robotic trajectories. We overcome the typical reactive nature of state-of-the-art trajectory planners by leveraging non-cooperative game theory to design a planner that encapsulates human-like features of preservation of a vital space, recognition of groups, sequential and strategized decision making, and smooth obstacle avoidance. Social acceptability is measured through a variation of the Turing test administered in the form of a survey questionnaire to a pool of 691 participants. Comparison terms for our tests are a state-of-the-art navigation algorithm (Enhanced Vector Field Histogram, VFH) and purely human trajectories. While all participants easily recognized the non-human nature of VFH-generated trajectories, the distinction between game-theoretical trajectories and human ones were hardly revealed. These results mark a strong milestone toward the full integration of robots in social environments.

Generative Adversarial Networks as stochastic Nash games

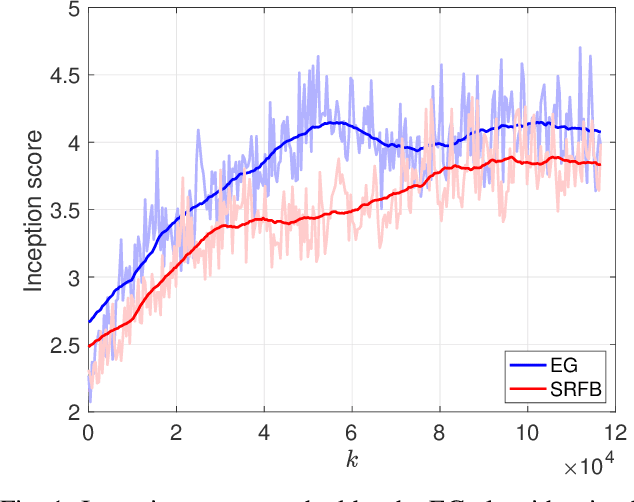
Generative adversarial networks (GANs) are a class of generative models with two antagonistic neural networks: the generator and the discriminator. These two neural networks compete against each other through an adversarial process that can be modelled as a stochastic Nash equilibrium problem. Since the associated training process is challenging, it is fundamental to design reliable algorithms to compute an equilibrium. In this paper, we propose a stochastic relaxed forward-backward algorithm for GANs and we show convergence to an exact solution or to a neighbourhood of it, if the pseudogradient mapping of the game is monotone. We apply our algorithm to the image generation problem where we observe computational advantages with respect to the extragradient scheme.

A game-theoretic approach for Generative Adversarial Networks

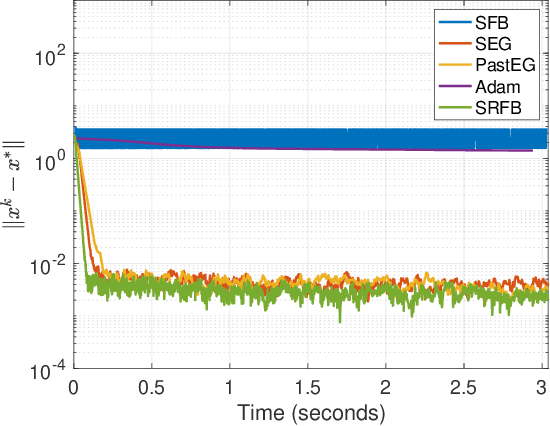
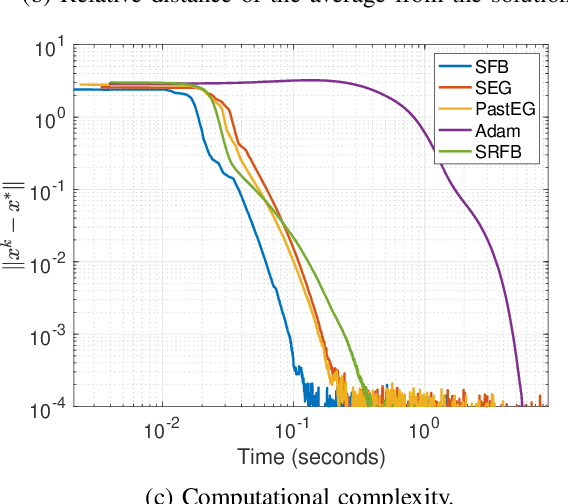
Generative adversarial networks (GANs) are a class of generative models, known for producing accurate samples. The key feature of GANs is that there are two antagonistic neural networks: the generator and the discriminator. The main bottleneck for their implementation is that the neural networks are very hard to train. One way to improve their performance is to design reliable algorithms for the adversarial process. Since the training can be cast as a stochastic Nash equilibrium problem, we rewrite it as a variational inequality and introduce an algorithm to compute an approximate solution. Specifically, we propose a stochastic relaxed forward-backward algorithm for GANs. We prove that when the pseudogradient mapping of the game is monotone, we have convergence to an exact solution or in a neighbourhood of it.