Generative Adversarial Networks as stochastic Nash games

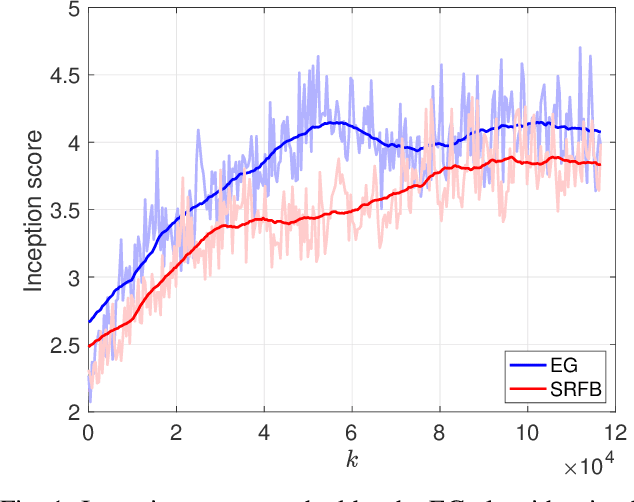
Generative adversarial networks (GANs) are a class of generative models with two antagonistic neural networks: the generator and the discriminator. These two neural networks compete against each other through an adversarial process that can be modelled as a stochastic Nash equilibrium problem. Since the associated training process is challenging, it is fundamental to design reliable algorithms to compute an equilibrium. In this paper, we propose a stochastic relaxed forward-backward algorithm for GANs and we show convergence to an exact solution or to a neighbourhood of it, if the pseudogradient mapping of the game is monotone. We apply our algorithm to the image generation problem where we observe computational advantages with respect to the extragradient scheme.