Reachability analysis in stochastic directed graphs by reinforcement learning

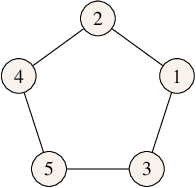
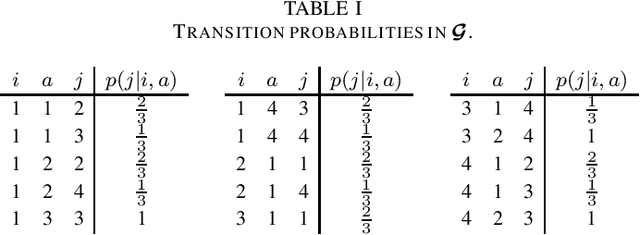
We characterize the reachability probabilities in stochastic directed graphs by means of reinforcement learning methods. In particular, we show that the dynamics of the transition probabilities in a stochastic digraph can be modeled via a difference inclusion, which, in turn, can be interpreted as a Markov decision process. Using the latter framework, we offer a methodology to design reward functions to provide upper and lower bounds on the reachability probabilities of a set of nodes for stochastic digraphs. The effectiveness of the proposed technique is demonstrated by application to the diffusion of epidemic diseases over time-varying contact networks generated by the proximity patterns of mobile agents.

A Universal Approximation Result for Difference of log-sum-exp Neural Networks

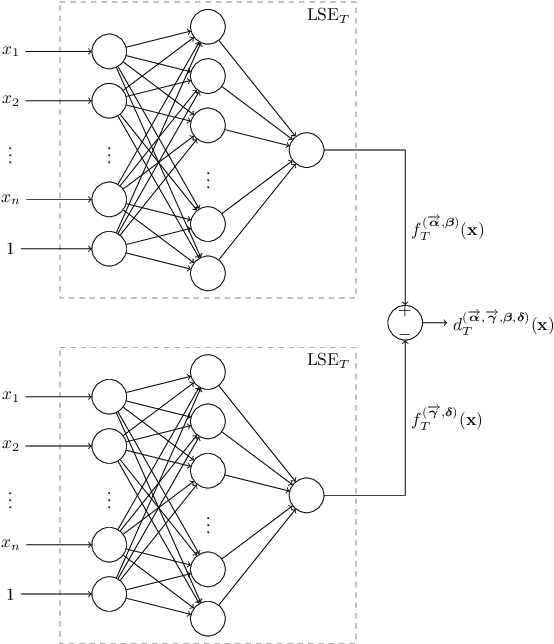
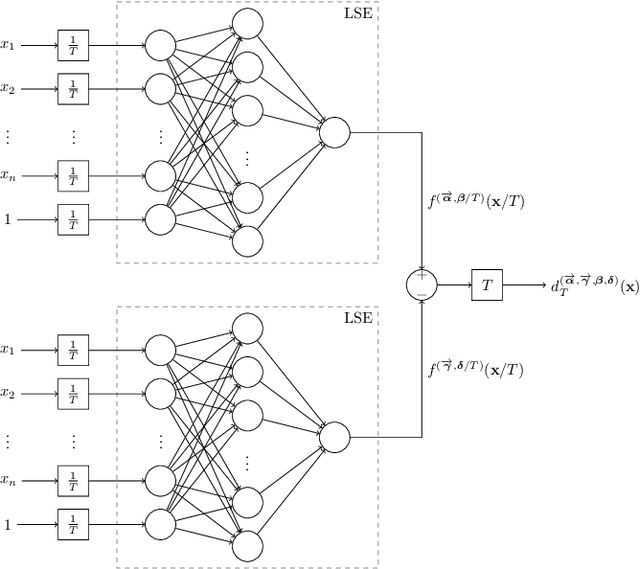
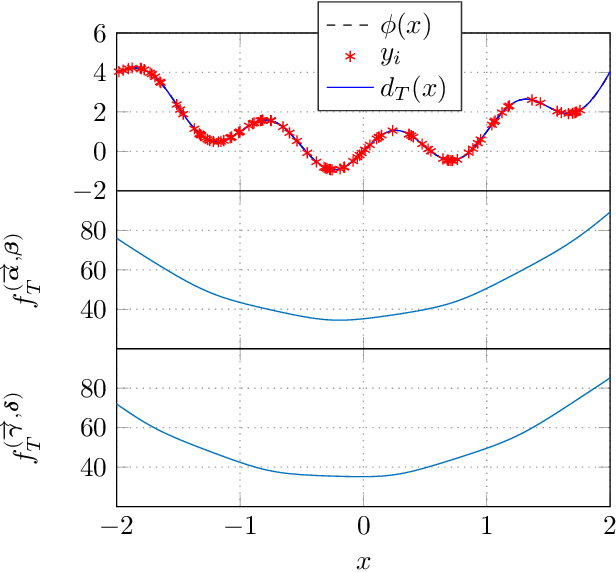
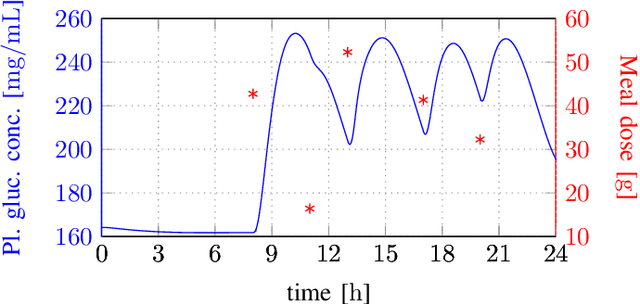
We show that a neural network whose output is obtained as the difference of the outputs of two feedforward networks with exponential activation function in the hidden layer and logarithmic activation function in the output node (LSE networks) is a smooth universal approximator of continuous functions over convex, compact sets. By using a logarithmic transform, this class of networks maps to a family of subtraction-free ratios of generalized posynomials, which we also show to be universal approximators of positive functions over log-convex, compact subsets of the positive orthant. The main advantage of Difference-LSE networks with respect to classical feedforward neural networks is that, after a standard training phase, they provide surrogate models for design that possess a specific difference-of-convex-functions form, which makes them optimizable via relatively efficient numerical methods. In particular, by adapting an existing difference-of-convex algorithm to these models, we obtain an algorithm for performing effective optimization-based design. We illustrate the proposed approach by applying it to data-driven design of a diet for a patient with type-2 diabetes.

Log-sum-exp neural networks and posynomial models for convex and log-log-convex data

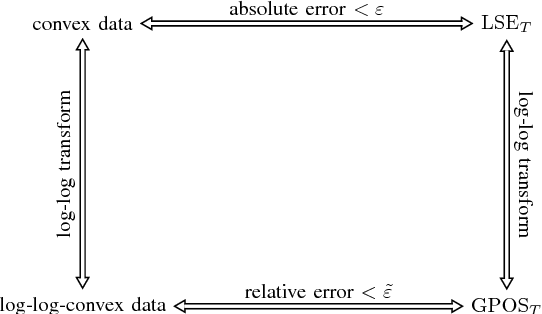
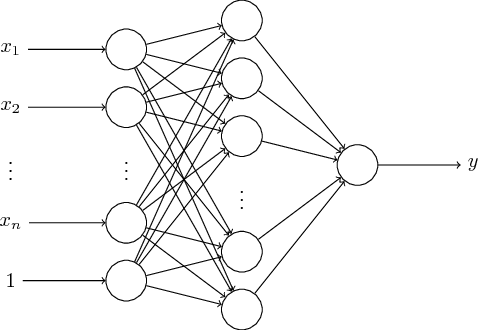
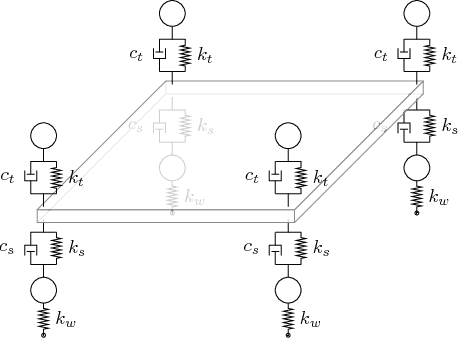
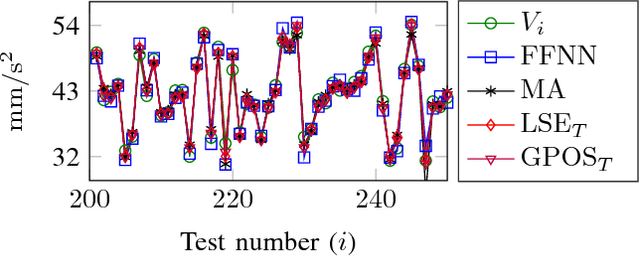
We show that a one-layer feedforward neural network with exponential activation functions in the inner layer and logarithmic activation in the output neuron is a universal approximator of convex functions. Such a network represents a family of scaled log-sum exponential functions, here named LSET. The proof uses a dequantization argument from tropical geometry. Under a suitable exponential transformation LSE maps to a family of generalized posynomial functions GPOST, which we also show to be universal approximators for log-log-convex functions. The key feature of interest in the proposed approach is that, once a LSET network is trained on data, the resulting model is convex in the variables, which makes it readily amenable to efficient design based on convex optimization. Similarly, once a GPOST model is trained on data, it yields a posynomial model that can be efficiently optimized with respect to its variables by using Geometric Programming (GP). Many relevant phenomena in physics and engineering can indeed be modeled, either exactly or approximately, via convex or log-log-convex models. The proposed methodology is illustrated by two numerical examples in which LSET and GPOST models are used to first approximate data gathered from the simulations of two physical processes (the vibration from a vehicle suspension system, and the peak power generated by the combustion of propane), and to later optimize these models.