Geometry-Aware Set-Membership Multilateration: Directional Bounds and Anchor Selection

In this paper, we study anchor selection for range-based localization under unknown-but-bounded measurement errors. We start from the convex localization set $\X=\Xd\cap\Hset$ recently introduced in \cite{CalafioreSIAM}, where $\Xd$ is a polyhedron obtained from pairwise differences of squared-range equations between the unknown location $x$ and the anchors, and $\Hset$ is the intersection of upper-range hyperspheres. Our first goal is \emph{offline} design: we derive geometry-only E- and D-type scores from the centered scatter matrix $S(A)=AQ_mA\tran$, where $A$ collects the anchor coordinates and $Q_m=I_m-\frac{1}{m}\one\one\tran$ is the centering projector, showing that $λ_{\min}(S(A))$ controls worst-direction and diameter surrogates for the polyhedral certificate $\Xd$, while $\det S(A)$ controls principal-axis volume surrogates. Our second goal is \emph{online} uncertainty assessment for a selected subset of anchors: exploiting the special structure $\X=\Xd\cap\Hset$, we derive a simplex-aggregated enclosing ball for $\Hset$ and an exact support-function formula for $\Hset$, which lead to finite hybrid bounds for the actual localization set $\X$, even when the polyhedral certificate deteriorates. Numerical experiments are performed in two dimensions, showing that geometry-based subset selection is close to an oracle combinatorial search, that the D-score slightly dominates the E-score for the area-oriented metric considered here, and that the new $\Hset$-aware certificates track the realized size of the selected localization set closely.

Playing the Lottery With Concave Regularizers for Sparse Trainable Neural Networks

The design of sparse neural networks, i.e., of networks with a reduced number of parameters, has been attracting increasing research attention in the last few years. The use of sparse models may significantly reduce the computational and storage footprint in the inference phase. In this context, the lottery ticket hypothesis (LTH) constitutes a breakthrough result, that addresses not only the performance of the inference phase, but also of the training phase. It states that it is possible to extract effective sparse subnetworks, called winning tickets, that can be trained in isolation. The development of effective methods to play the lottery, i.e., to find winning tickets, is still an open problem. In this article, we propose a novel class of methods to play the lottery. The key point is the use of concave regularization to promote the sparsity of a relaxed binary mask, which represents the network topology. We theoretically analyze the effectiveness of the proposed method in the convex framework. Then, we propose extended numerical tests on various datasets and architectures, that show that the proposed method can improve the performance of state-of-the-art algorithms.

Sparse $\ell_1$ and $\ell_2$ Center Classifiers

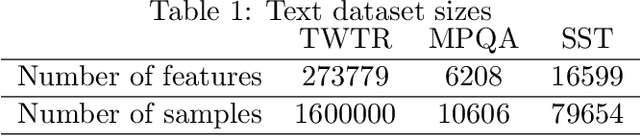
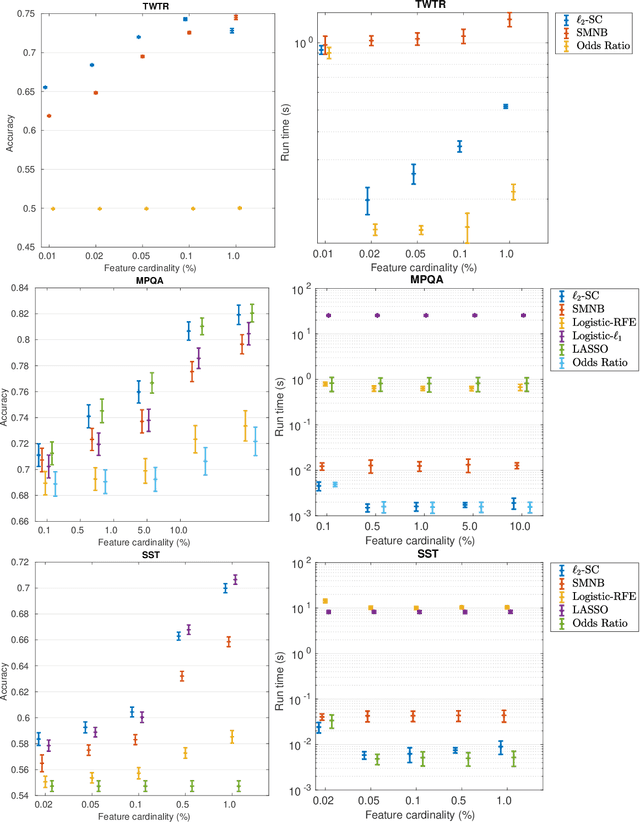
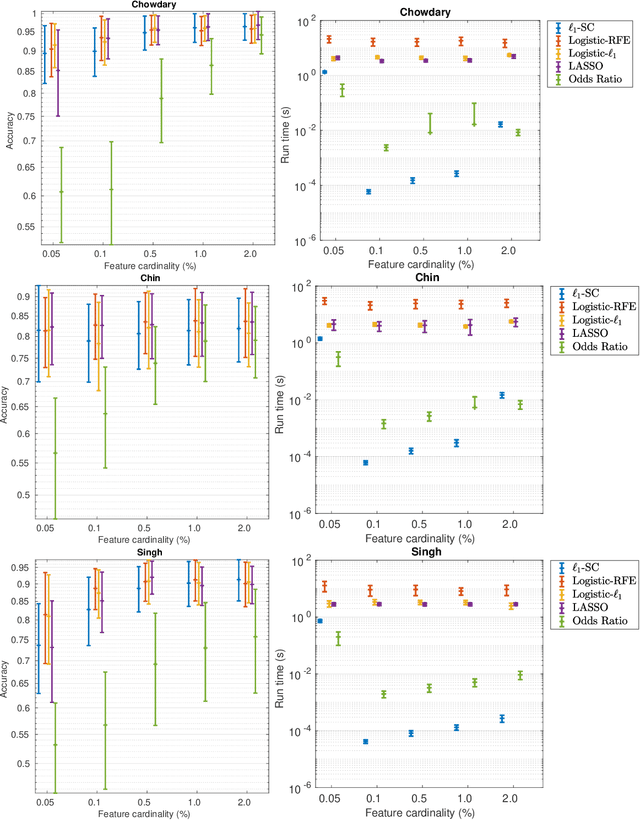
The nearest-centroid classifier is a simple linear-time classifier based on computing the centroids of the data classes in the training phase, and then assigning a new datum to the class corresponding to its nearest centroid. Thanks to its very low computational cost, the nearest-centroid classifier is still widely used in machine learning, despite the development of many other more sophisticated classification methods. In this paper, we propose two sparse variants of the nearest-centroid classifier, based respectively on $\ell_1$ and $\ell_2$ distance criteria. The proposed sparse classifiers perform simultaneous classification and feature selection, by detecting the features that are most relevant for the classification purpose. We show that training of the proposed sparse models, with both distance criteria, can be performed exactly (i.e., the globally optimal set of features is selected) and at a quasi-linear computational cost. The experimental results show that the proposed methods are competitive in accuracy with state-of-the-art feature selection techniques, while having a significantly lower computational cost.

Survival and Neural Models for Private Equity Exit Prediction

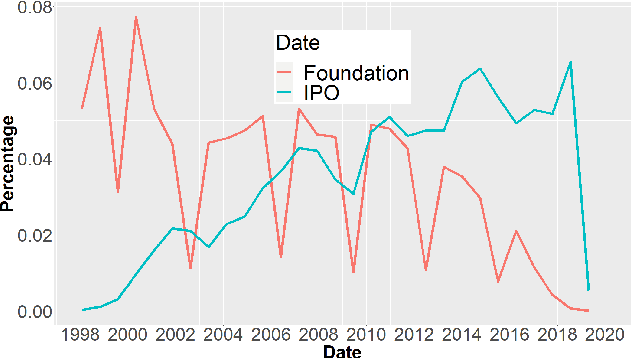
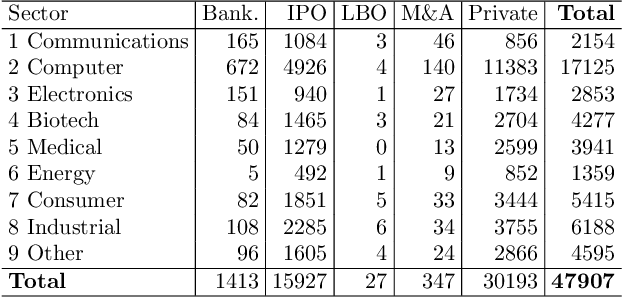
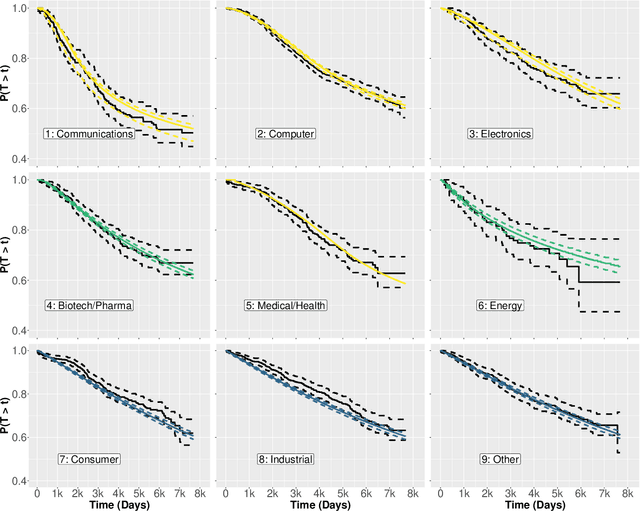
Within the Private Equity (PE) market, the event of a private company undertaking an Initial Public Offering (IPO) is usually a very high-return one for the investors in the company. For this reason, an effective predictive model for the IPO event is considered as a valuable tool in the PE market, an endeavor in which publicly available quantitative information is generally scarce. In this paper, we describe a data-analytic procedure for predicting the probability with which a company will go public in a given forward period of time. The proposed method is based on the interplay of a neural network (NN) model for estimating the overall event probability, and Survival Analysis (SA) for further modeling the probability of the IPO event in any given interval of time. The proposed neuro-survival model is tuned and tested across nine industrial sectors using real data from the Thomson Reuters Eikon PE database.

A Universal Approximation Result for Difference of log-sum-exp Neural Networks

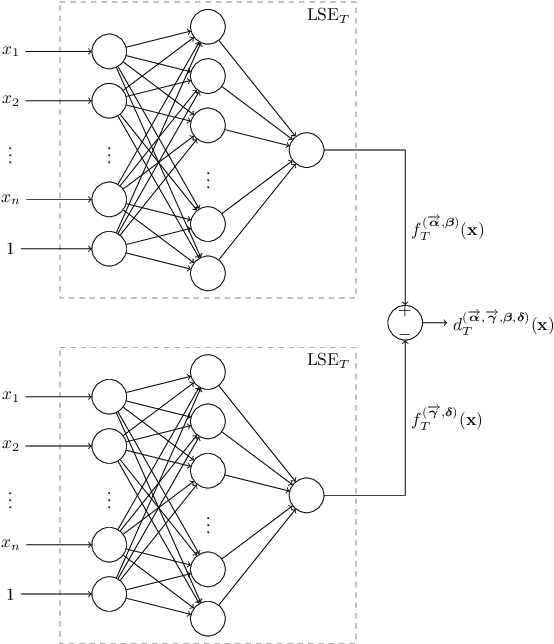
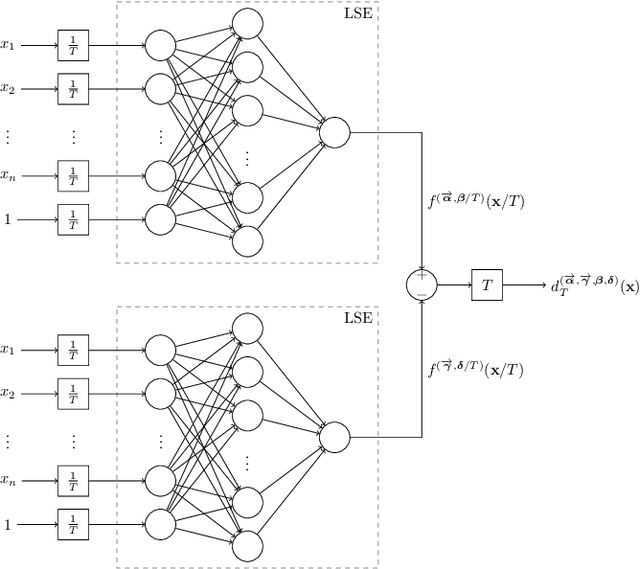
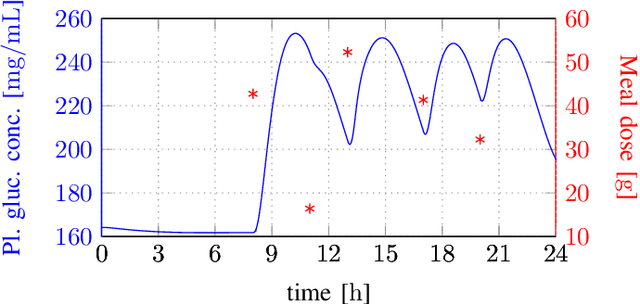
We show that a neural network whose output is obtained as the difference of the outputs of two feedforward networks with exponential activation function in the hidden layer and logarithmic activation function in the output node (LSE networks) is a smooth universal approximator of continuous functions over convex, compact sets. By using a logarithmic transform, this class of networks maps to a family of subtraction-free ratios of generalized posynomials, which we also show to be universal approximators of positive functions over log-convex, compact subsets of the positive orthant. The main advantage of Difference-LSE networks with respect to classical feedforward neural networks is that, after a standard training phase, they provide surrogate models for design that possess a specific difference-of-convex-functions form, which makes them optimizable via relatively efficient numerical methods. In particular, by adapting an existing difference-of-convex algorithm to these models, we obtain an algorithm for performing effective optimization-based design. We illustrate the proposed approach by applying it to data-driven design of a diet for a patient with type-2 diabetes.

Log-sum-exp neural networks and posynomial models for convex and log-log-convex data

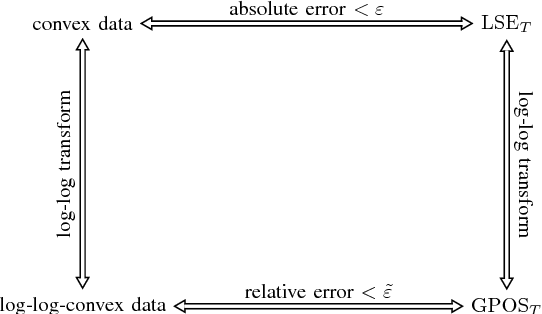
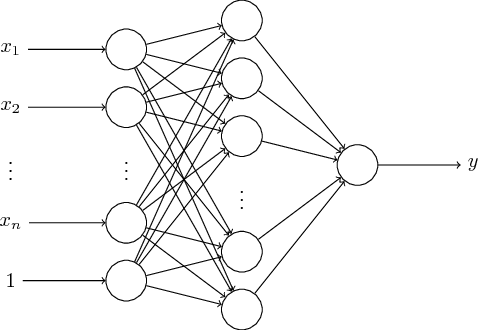
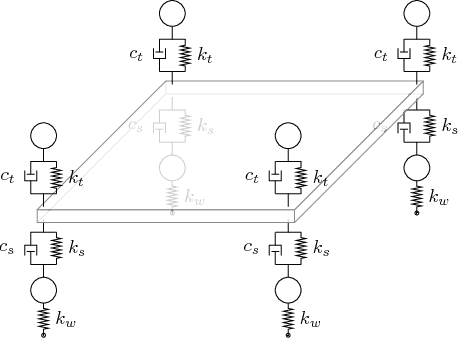
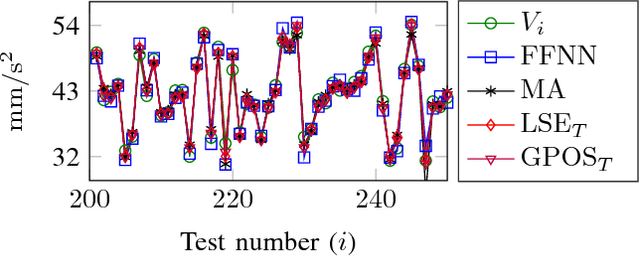
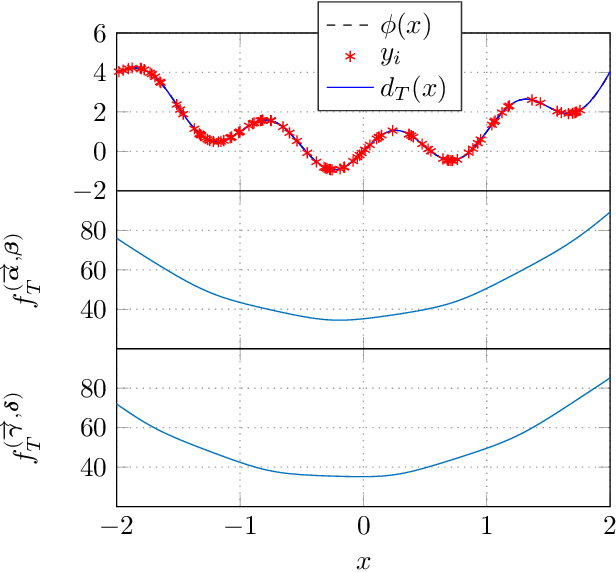
We show that a one-layer feedforward neural network with exponential activation functions in the inner layer and logarithmic activation in the output neuron is a universal approximator of convex functions. Such a network represents a family of scaled log-sum exponential functions, here named LSET. The proof uses a dequantization argument from tropical geometry. Under a suitable exponential transformation LSE maps to a family of generalized posynomial functions GPOST, which we also show to be universal approximators for log-log-convex functions. The key feature of interest in the proposed approach is that, once a LSET network is trained on data, the resulting model is convex in the variables, which makes it readily amenable to efficient design based on convex optimization. Similarly, once a GPOST model is trained on data, it yields a posynomial model that can be efficiently optimized with respect to its variables by using Geometric Programming (GP). Many relevant phenomena in physics and engineering can indeed be modeled, either exactly or approximately, via convex or log-log-convex models. The proposed methodology is illustrated by two numerical examples in which LSET and GPOST models are used to first approximate data gathered from the simulations of two physical processes (the vibration from a vehicle suspension system, and the peak power generated by the combustion of propane), and to later optimize these models.

Convex Relaxations for Pose Graph Optimization with Outliers

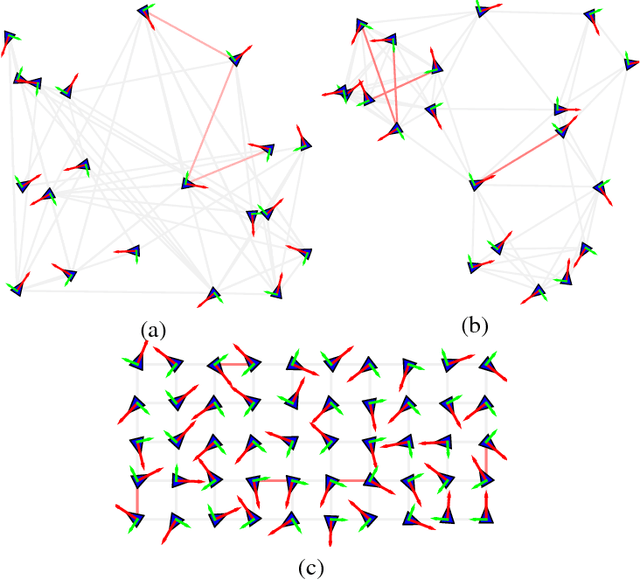
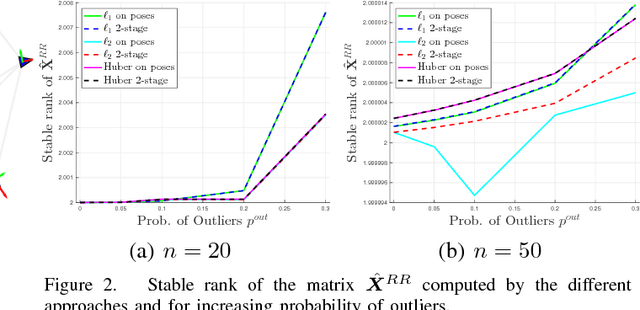
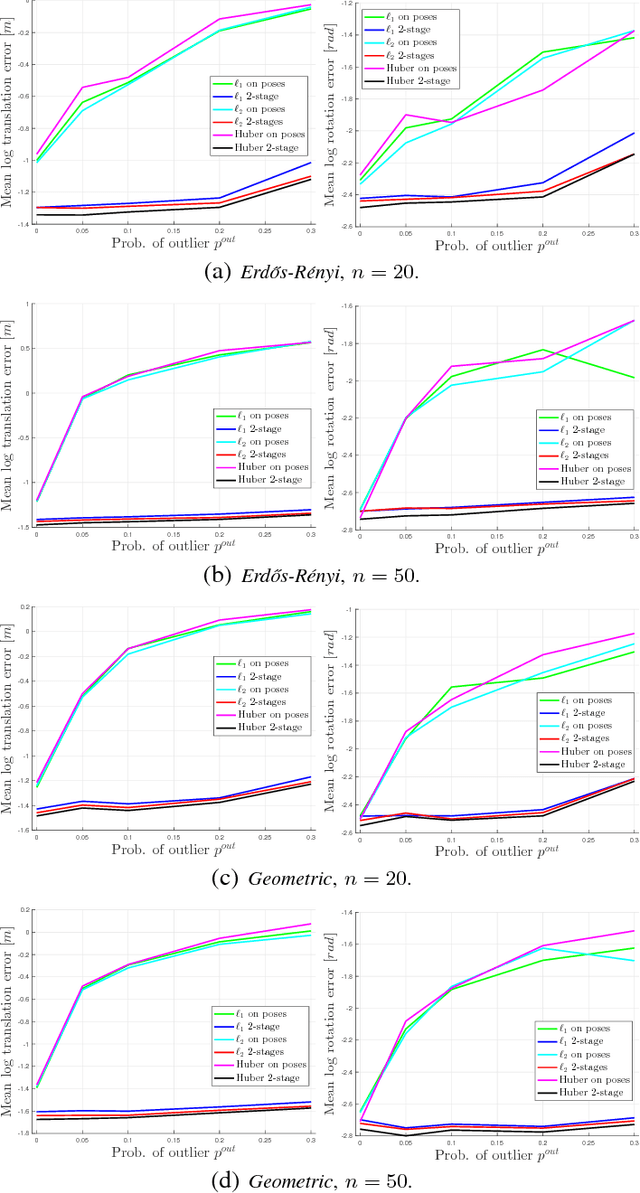
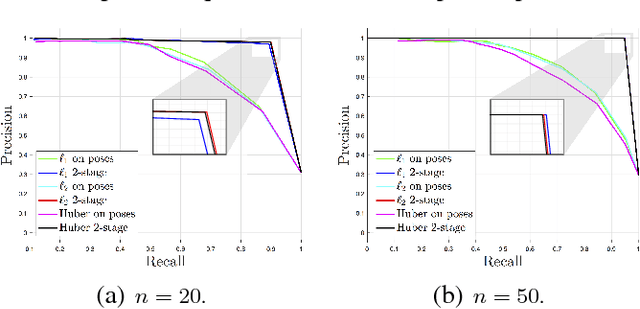
Pose Graph Optimization involves the estimation of a set of poses from pairwise measurements and provides a formalization for many problems arising in mobile robotics and geometric computer vision. In this paper, we consider the case in which a subset of the measurements fed to pose graph optimization is spurious. Our first contribution is to develop robust estimators that can cope with heavy-tailed measurement noise, hence increasing robustness to the presence of outliers. Since the resulting estimators require solving nonconvex optimization problems, we further develop convex relaxations that approximately solve those problems via semidefinite programming. We then provide conditions under which the proposed relaxations are exact. Contrarily to existing approaches, our convex relaxations do not rely on the availability of an initial guess for the unknown poses, hence they are more suitable for setups in which such guess is not available (e.g., multi-robot localization, recovery after localization failure). We tested the proposed techniques in extensive simulations, and we show that some of the proposed relaxations are indeed tight (i.e., they solve the original nonconvex problem 10 exactly) and ensure accurate estimation in the face of a large number of outliers.