Convex Relaxations for Pose Graph Optimization with Outliers
Paper and Code
Jan 07, 2018
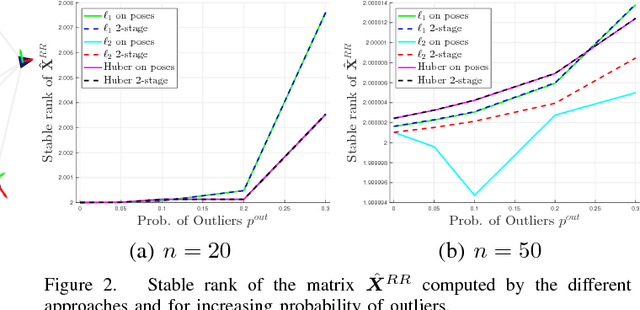
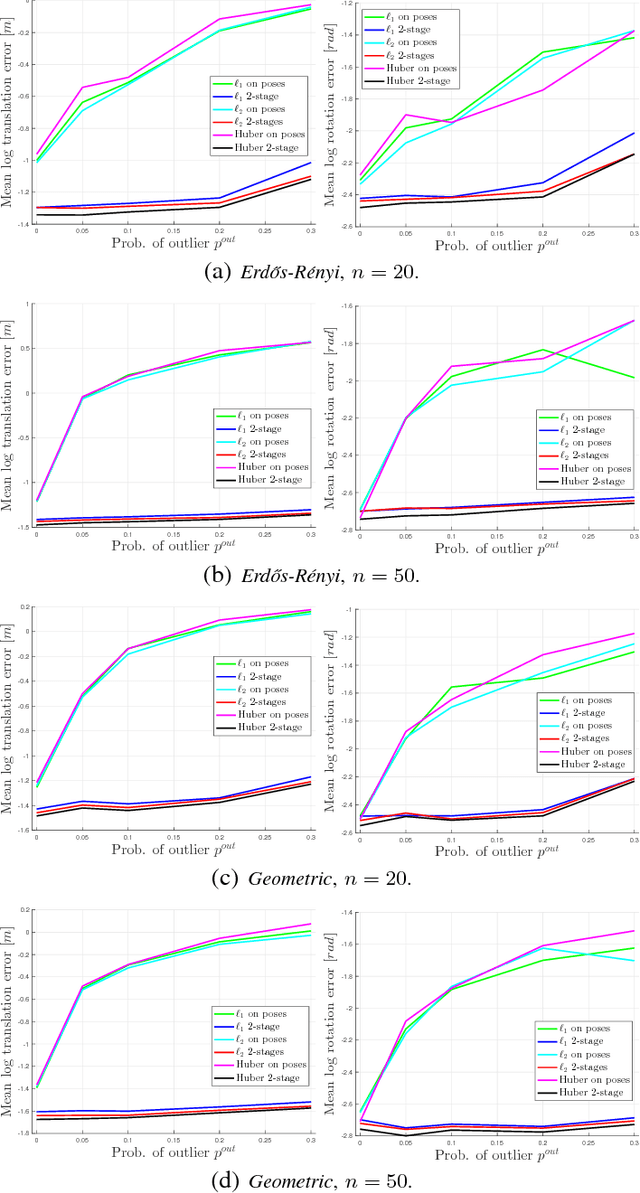
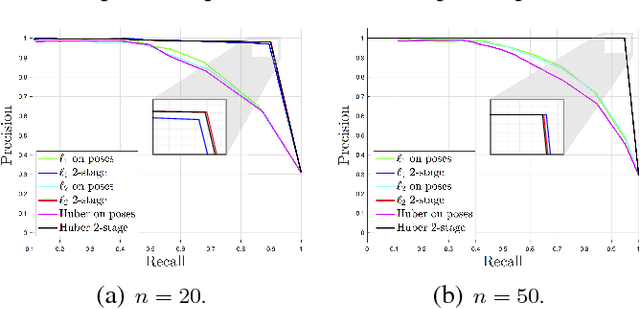
Pose Graph Optimization involves the estimation of a set of poses from pairwise measurements and provides a formalization for many problems arising in mobile robotics and geometric computer vision. In this paper, we consider the case in which a subset of the measurements fed to pose graph optimization is spurious. Our first contribution is to develop robust estimators that can cope with heavy-tailed measurement noise, hence increasing robustness to the presence of outliers. Since the resulting estimators require solving nonconvex optimization problems, we further develop convex relaxations that approximately solve those problems via semidefinite programming. We then provide conditions under which the proposed relaxations are exact. Contrarily to existing approaches, our convex relaxations do not rely on the availability of an initial guess for the unknown poses, hence they are more suitable for setups in which such guess is not available (e.g., multi-robot localization, recovery after localization failure). We tested the proposed techniques in extensive simulations, and we show that some of the proposed relaxations are indeed tight (i.e., they solve the original nonconvex problem 10 exactly) and ensure accurate estimation in the face of a large number of outliers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge