Fast sparse optimization via adaptive shrinkage

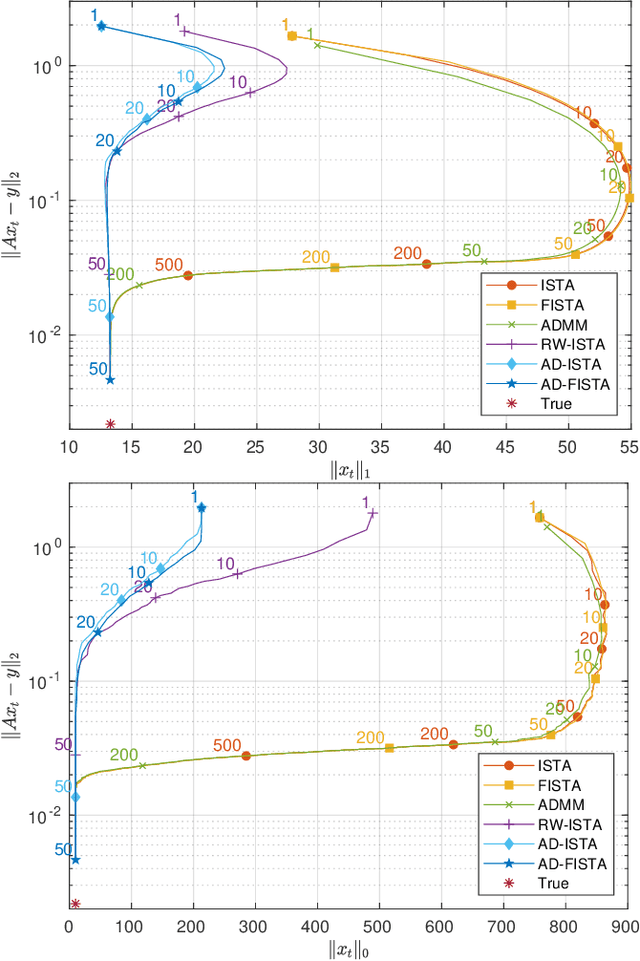
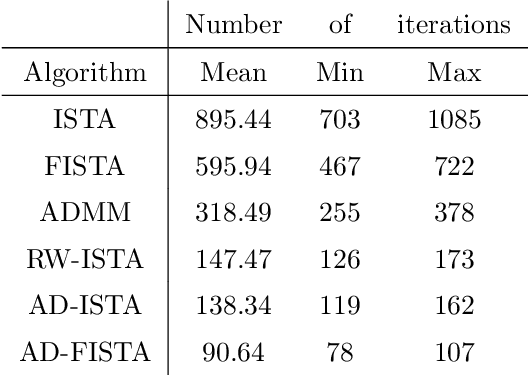
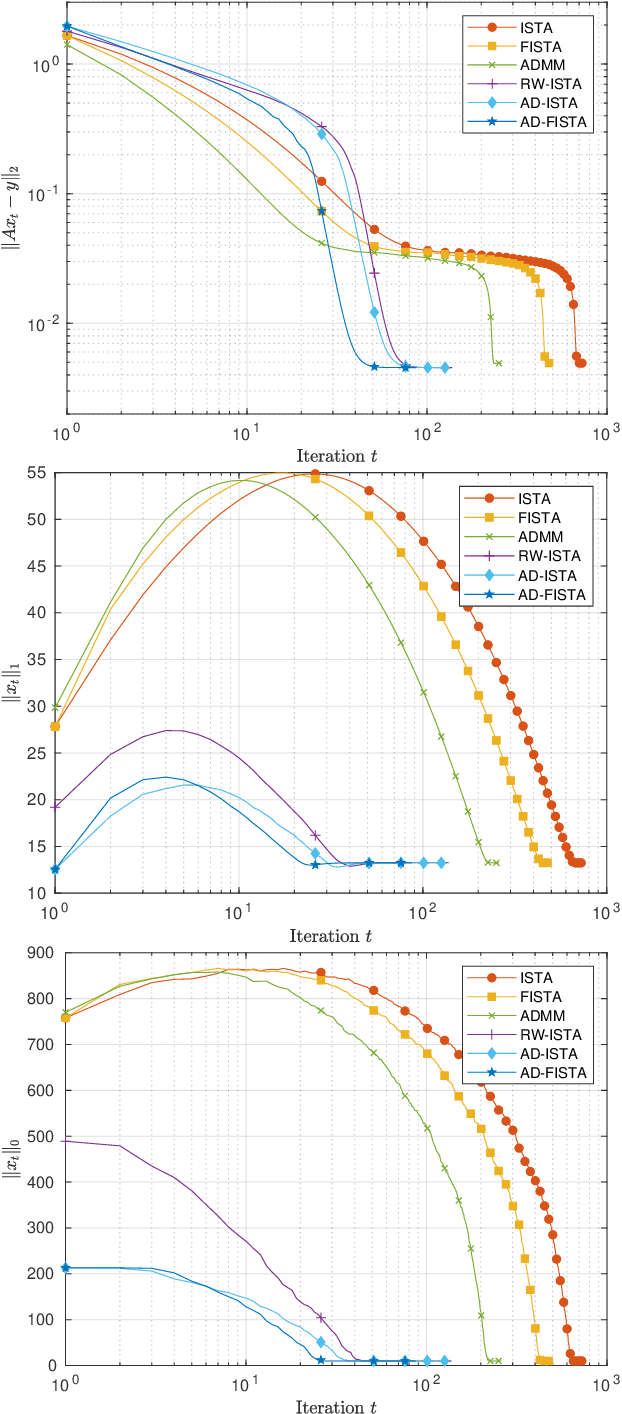
The need for fast sparse optimization is emerging, e.g., to deal with large-dimensional data-driven problems and to track time-varying systems. In the framework of linear sparse optimization, the iterative shrinkage-thresholding algorithm is a valuable method to solve Lasso, which is particularly appreciated for its ease of implementation. Nevertheless, it converges slowly. In this paper, we develop a proximal method, based on logarithmic regularization, which turns out to be an iterative shrinkage-thresholding algorithm with adaptive shrinkage hyperparameter. This adaptivity substantially enhances the trajectory of the algorithm, in a way that yields faster convergence, while keeping the simplicity of the original method. Our contribution is twofold: on the one hand, we derive and analyze the proposed algorithm; on the other hand, we validate its fast convergence via numerical experiments and we discuss the performance with respect to state-of-the-art algorithms.

Playing the Lottery With Concave Regularizers for Sparse Trainable Neural Networks

The design of sparse neural networks, i.e., of networks with a reduced number of parameters, has been attracting increasing research attention in the last few years. The use of sparse models may significantly reduce the computational and storage footprint in the inference phase. In this context, the lottery ticket hypothesis (LTH) constitutes a breakthrough result, that addresses not only the performance of the inference phase, but also of the training phase. It states that it is possible to extract effective sparse subnetworks, called winning tickets, that can be trained in isolation. The development of effective methods to play the lottery, i.e., to find winning tickets, is still an open problem. In this article, we propose a novel class of methods to play the lottery. The key point is the use of concave regularization to promote the sparsity of a relaxed binary mask, which represents the network topology. We theoretically analyze the effectiveness of the proposed method in the convex framework. Then, we propose extended numerical tests on various datasets and architectures, that show that the proposed method can improve the performance of state-of-the-art algorithms.

Centralized and distributed online learning for sparse time-varying optimization

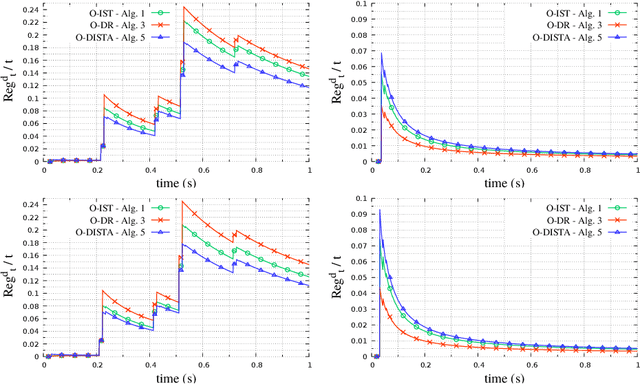
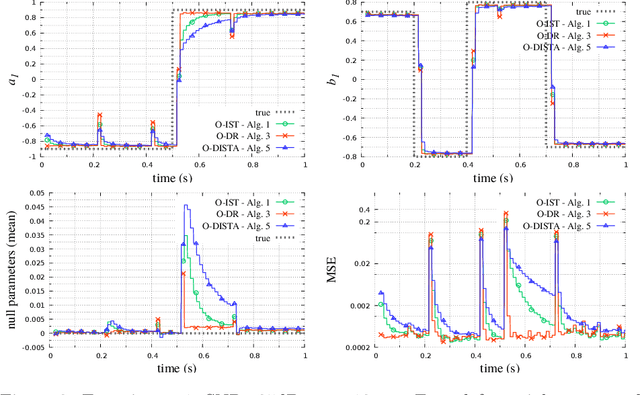
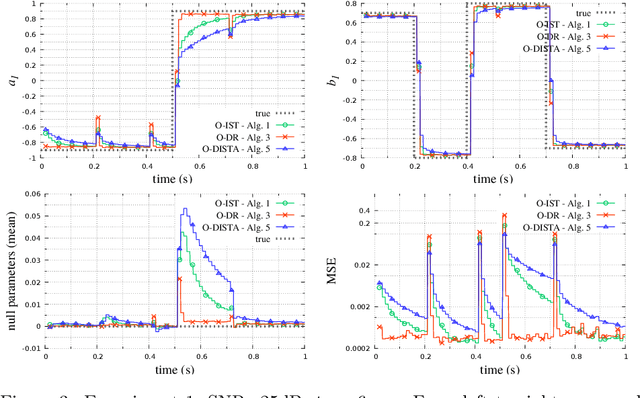
The development of online algorithms to track time-varying systems has drawn a lot of attention in the last years, in particular in the framework of online convex optimization. Meanwhile, sparse time-varying optimization has emerged as a powerful tool to deal with widespread applications, ranging from dynamic compressed sensing to parsimonious system identification. In most of the literature on sparse time-varying problems, some prior information on the system's evolution is assumed to be available. In contrast, in this paper, we propose an online learning approach, which does not employ a given model and is suitable for adversarial frameworks. Specifically, we develop centralized and distributed algorithms, and we theoretically analyze them in terms of dynamic regret, in an online learning perspective. Further, we propose numerical experiments that illustrate their practical effectiveness.

Sparse linear regression with compressed and low-precision data via concave quadratic programming

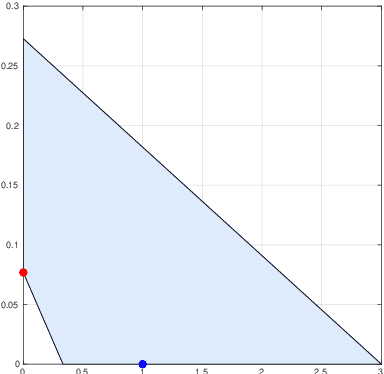
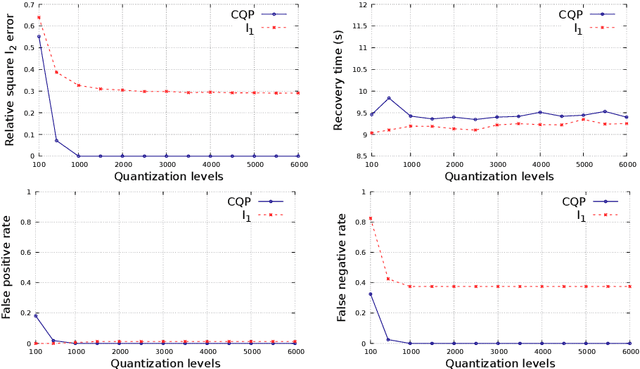
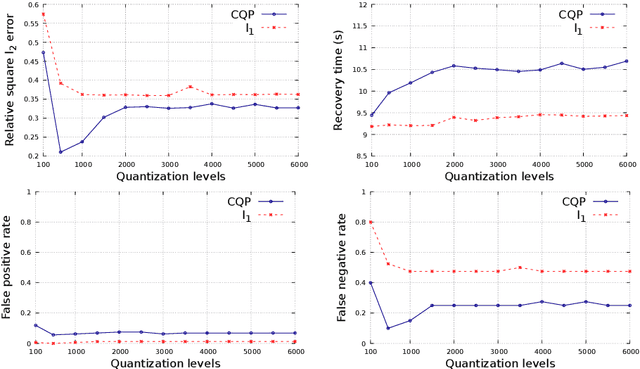
We consider the problem of the recovery of a k-sparse vector from compressed linear measurements when data are corrupted by a quantization noise. When the number of measurements is not sufficiently large, different $k$-sparse solutions may be present in the feasible set, and the classical l1 approach may be unsuccessful. For this motivation, we propose a non-convex quadratic programming method, which exploits prior information on the magnitude of the non-zero parameters. This results in a more efficient support recovery. We provide sufficient conditions for successful recovery and numerical simulations to illustrate the practical feasibility of the proposed method.

Recovery of binary sparse signals from compressed linear measurements via polynomial optimization

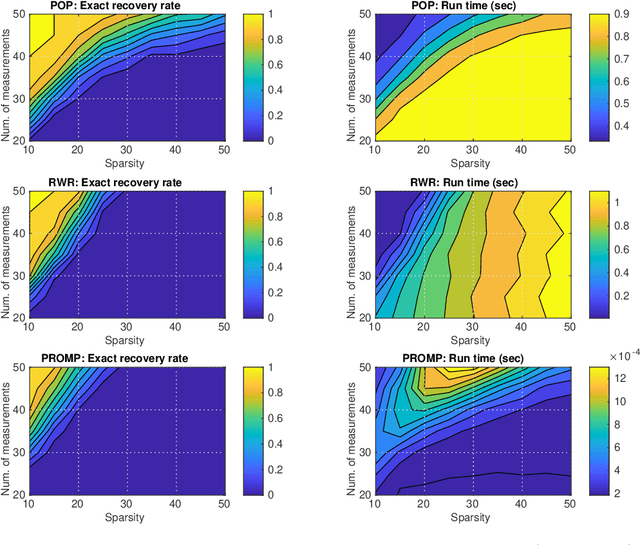
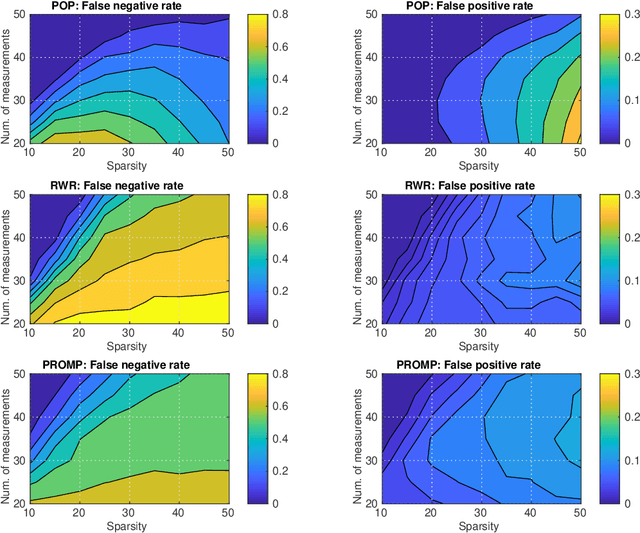
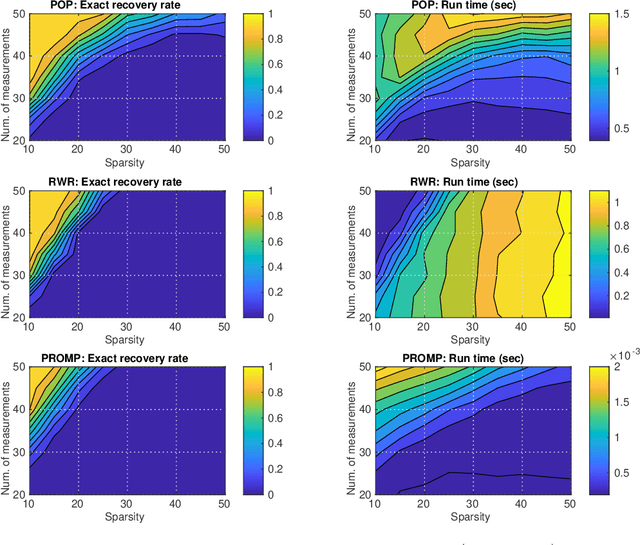
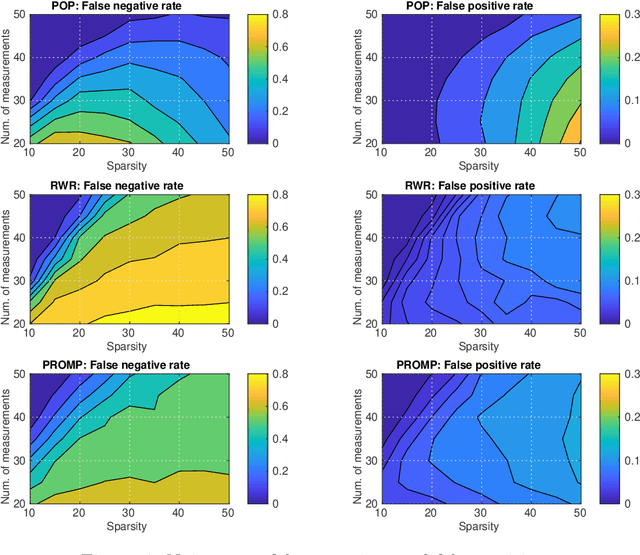
The recovery of signals with finite-valued components from few linear measurements is a problem with widespread applications and interesting mathematical characteristics. In the compressed sensing framework, tailored methods have been recently proposed to deal with the case of finite-valued sparse signals. In this work, we focus on binary sparse signals and we propose a novel formulation, based on polynomial optimization. This approach is analyzed and compared to the state-of-the-art binary compressed sensing methods.

A biconvex analysis for Lasso l1 reweighting

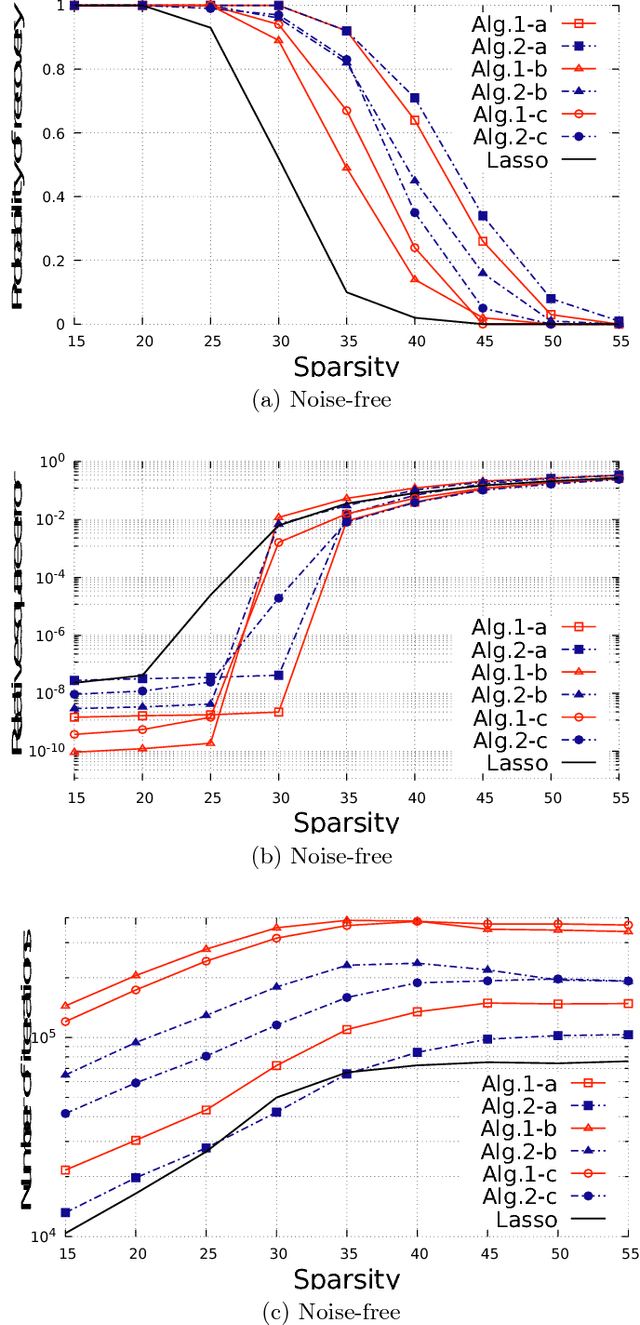
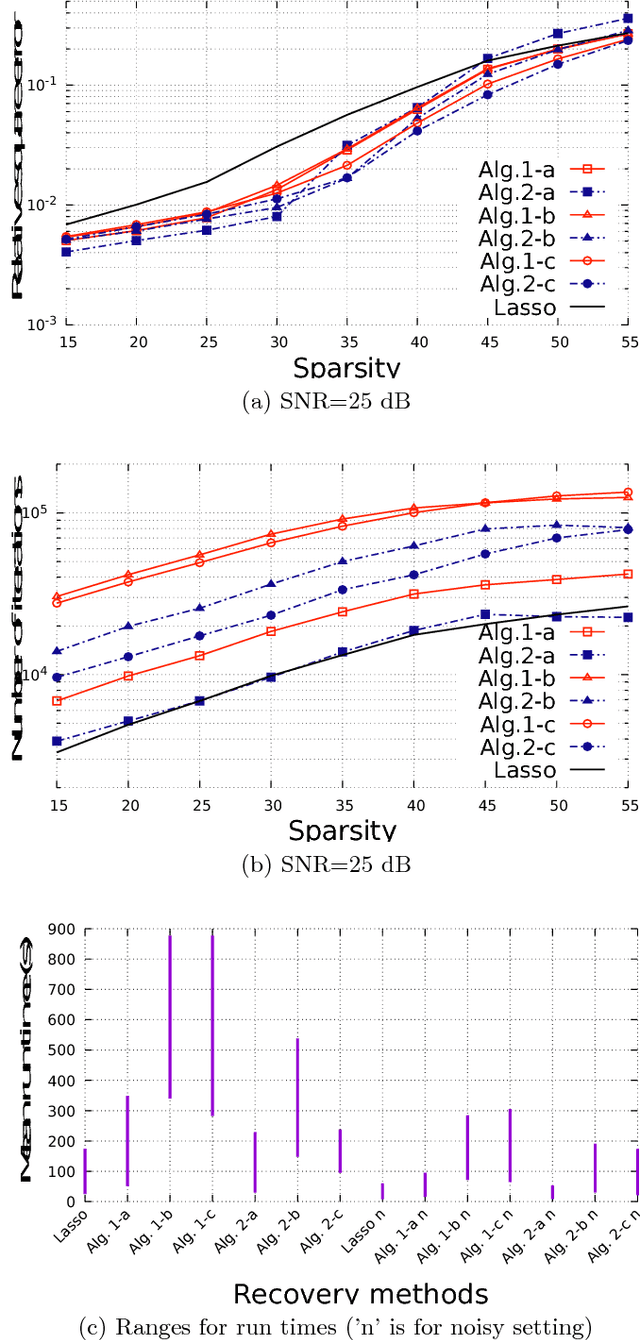
l1 reweighting algorithms are very popular in sparse signal recovery and compressed sensing, since in the practice they have been observed to outperform classical l1 methods. Nevertheless, the theoretical analysis of their convergence is a critical point, and generally is limited to the convergence of the functional to a local minimum or to subsequence convergence. In this letter, we propose a new convergence analysis of a Lasso l1 reweighting method, based on the observation that the algorithm is an alternated convex search for a biconvex problem. Based on that, we are able to prove the numerical convergence of the sequence of the iterates generated by the algorithm. This is not yet the convergence of the sequence, but it is close enough for practical and numerical purposes. Furthermore, we propose an alternative iterative soft thresholding procedure, which is faster than the main algorithm.

GPU-Accelerated Algorithms for Compressed Signals Recovery with Application to Astronomical Imagery Deblurring

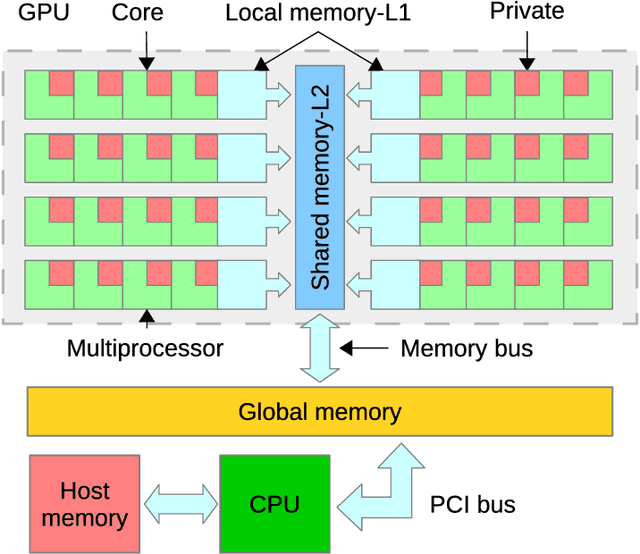
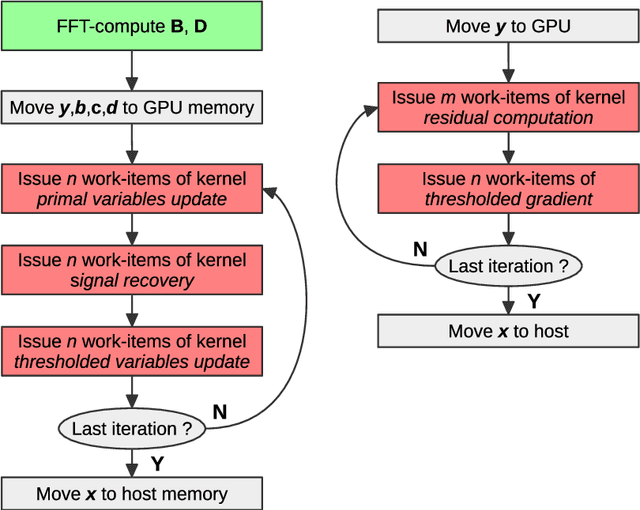
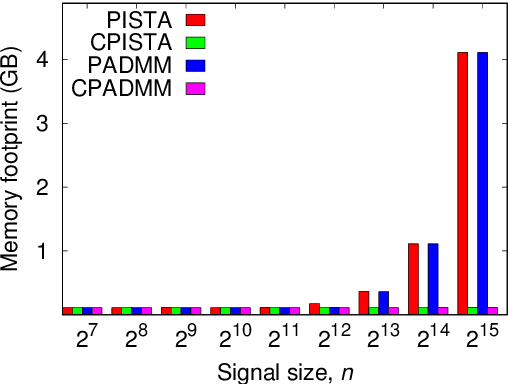
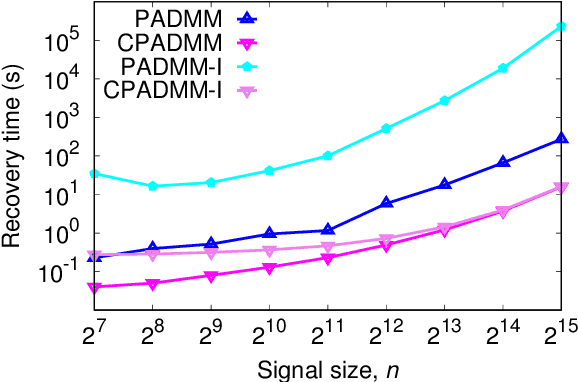
Compressive sensing promises to enable bandwidth-efficient on-board compression of astronomical data by lifting the encoding complexity from the source to the receiver. The signal is recovered off-line, exploiting GPUs parallel computation capabilities to speedup the reconstruction process. However, inherent GPU hardware constraints limit the size of the recoverable signal and the speedup practically achievable. In this work, we design parallel algorithms that exploit the properties of circulant matrices for efficient GPU-accelerated sparse signals recovery. Our approach reduces the memory requirements, allowing us to recover very large signals with limited memory. In addition, it achieves a tenfold signal recovery speedup thanks to ad-hoc parallelization of matrix-vector multiplications and matrix inversions. Finally, we practically demonstrate our algorithms in a typical application of circulant matrices: deblurring a sparse astronomical image in the compressed domain.