Analysis of SparseHash: an efficient embedding of set-similarity via sparse projections

Embeddings provide compact representations of signals in order to perform efficient inference in a wide variety of tasks. In particular, random projections are common tools to construct Euclidean distance-preserving embeddings, while hashing techniques are extensively used to embed set-similarity metrics, such as the Jaccard coefficient. In this letter, we theoretically prove that a class of random projections based on sparse matrices, called SparseHash, can preserve the Jaccard coefficient between the supports of sparse signals, which can be used to estimate set similarities. Moreover, besides the analysis, we provide an efficient implementation and we test the performance in several numerical experiments, both on synthetic and real datasets.

GPU-Accelerated Algorithms for Compressed Signals Recovery with Application to Astronomical Imagery Deblurring

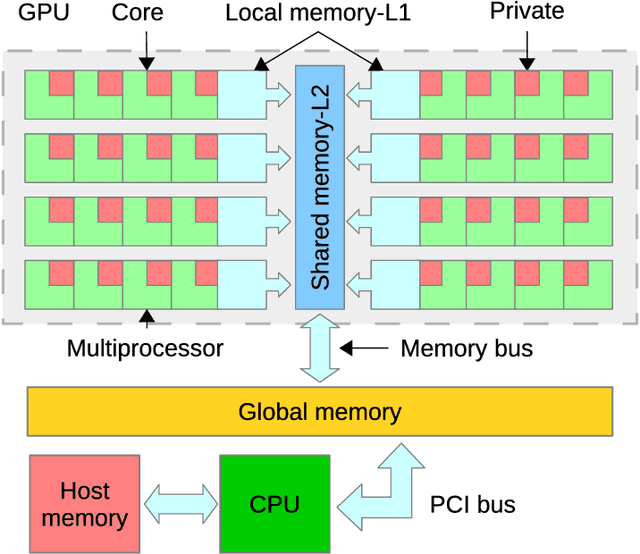
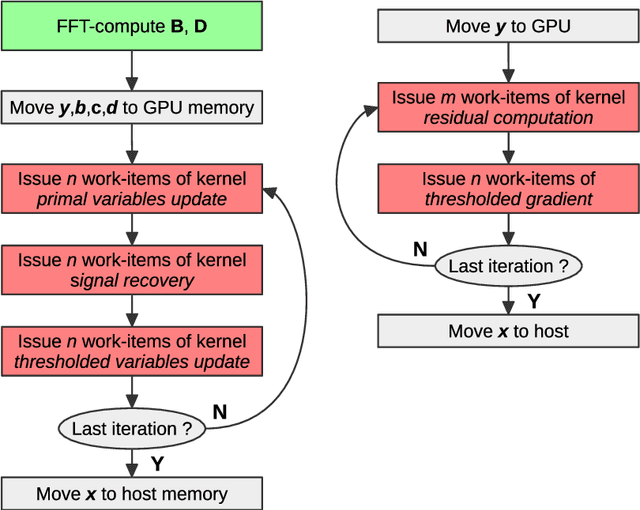
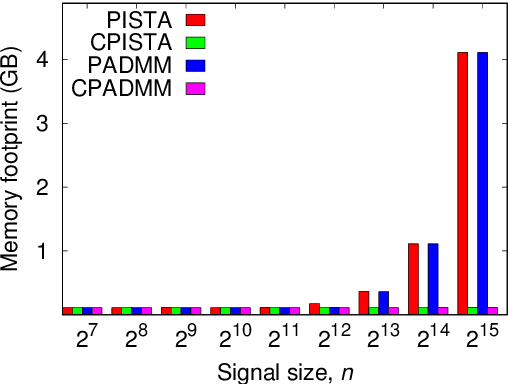
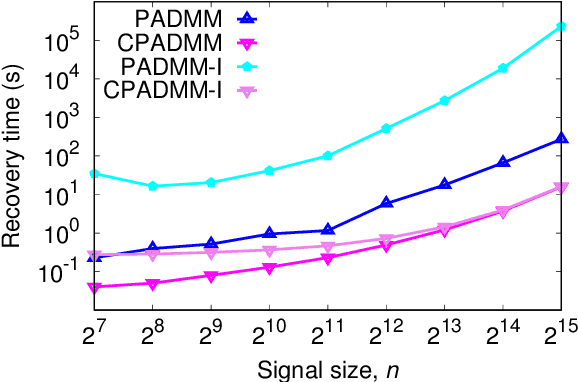
Compressive sensing promises to enable bandwidth-efficient on-board compression of astronomical data by lifting the encoding complexity from the source to the receiver. The signal is recovered off-line, exploiting GPUs parallel computation capabilities to speedup the reconstruction process. However, inherent GPU hardware constraints limit the size of the recoverable signal and the speedup practically achievable. In this work, we design parallel algorithms that exploit the properties of circulant matrices for efficient GPU-accelerated sparse signals recovery. Our approach reduces the memory requirements, allowing us to recover very large signals with limited memory. In addition, it achieves a tenfold signal recovery speedup thanks to ad-hoc parallelization of matrix-vector multiplications and matrix inversions. Finally, we practically demonstrate our algorithms in a typical application of circulant matrices: deblurring a sparse astronomical image in the compressed domain.