A biconvex analysis for Lasso l1 reweighting

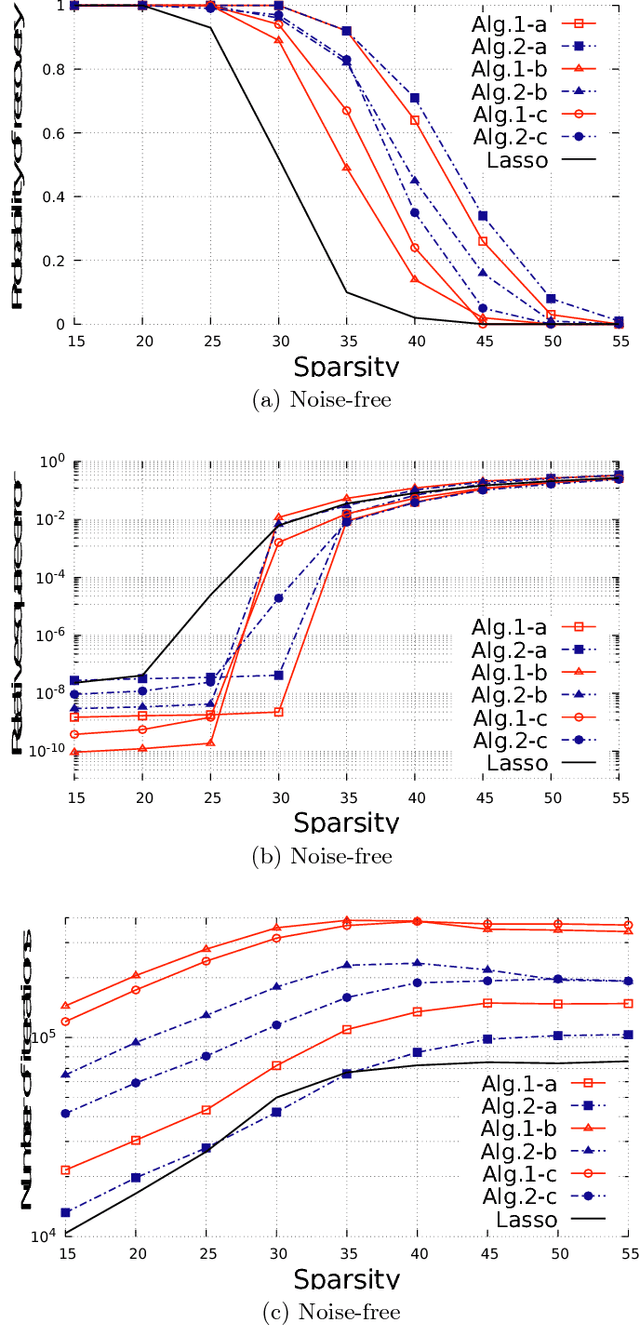
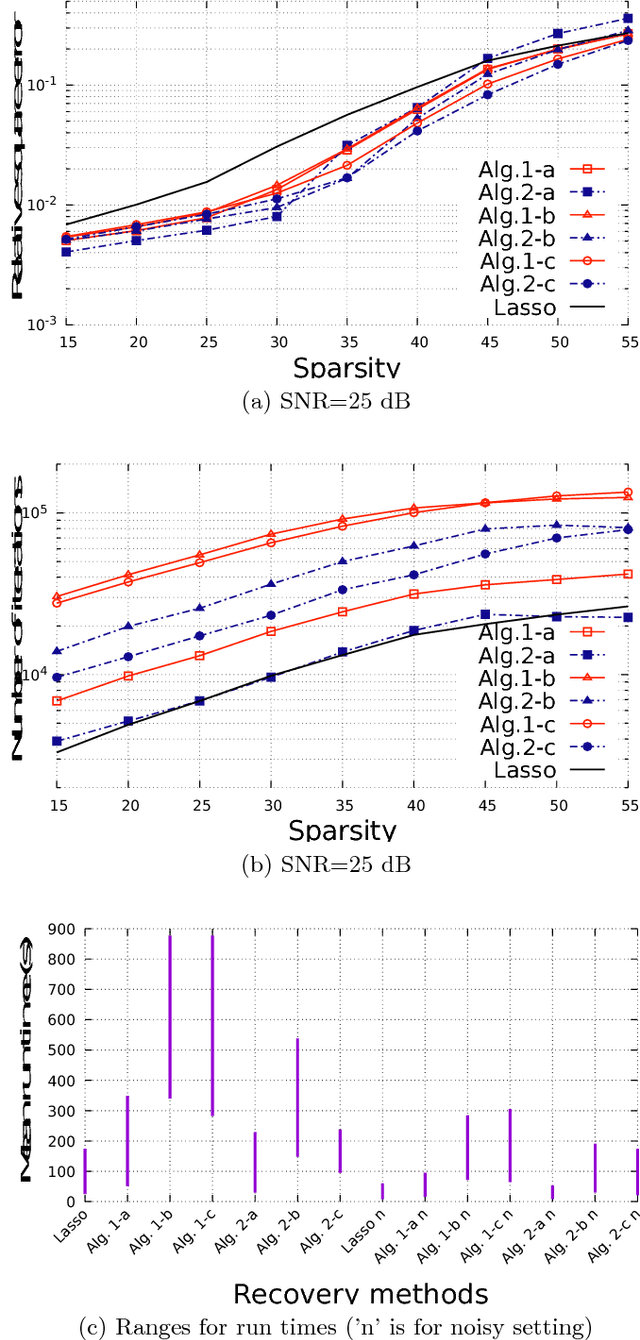
l1 reweighting algorithms are very popular in sparse signal recovery and compressed sensing, since in the practice they have been observed to outperform classical l1 methods. Nevertheless, the theoretical analysis of their convergence is a critical point, and generally is limited to the convergence of the functional to a local minimum or to subsequence convergence. In this letter, we propose a new convergence analysis of a Lasso l1 reweighting method, based on the observation that the algorithm is an alternated convex search for a biconvex problem. Based on that, we are able to prove the numerical convergence of the sequence of the iterates generated by the algorithm. This is not yet the convergence of the sequence, but it is close enough for practical and numerical purposes. Furthermore, we propose an alternative iterative soft thresholding procedure, which is faster than the main algorithm.