Fast sparse optimization via adaptive shrinkage

The need for fast sparse optimization is emerging, e.g., to deal with large-dimensional data-driven problems and to track time-varying systems. In the framework of linear sparse optimization, the iterative shrinkage-thresholding algorithm is a valuable method to solve Lasso, which is particularly appreciated for its ease of implementation. Nevertheless, it converges slowly. In this paper, we develop a proximal method, based on logarithmic regularization, which turns out to be an iterative shrinkage-thresholding algorithm with adaptive shrinkage hyperparameter. This adaptivity substantially enhances the trajectory of the algorithm, in a way that yields faster convergence, while keeping the simplicity of the original method. Our contribution is twofold: on the one hand, we derive and analyze the proposed algorithm; on the other hand, we validate its fast convergence via numerical experiments and we discuss the performance with respect to state-of-the-art algorithms.

Sparse linear regression with compressed and low-precision data via concave quadratic programming

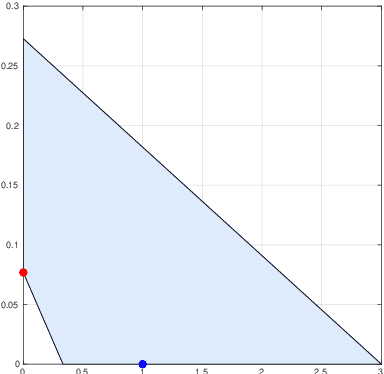
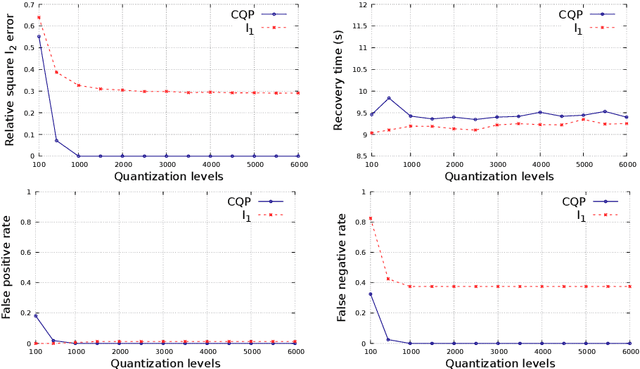
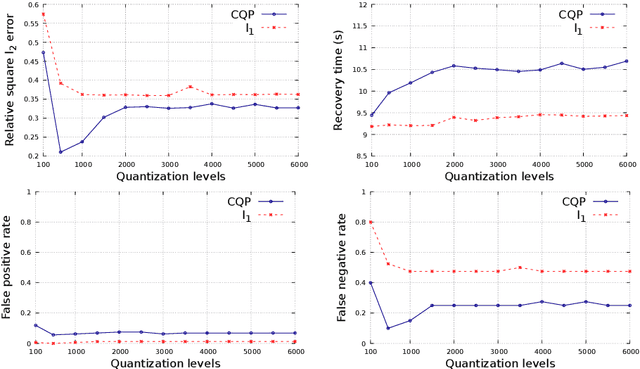
We consider the problem of the recovery of a k-sparse vector from compressed linear measurements when data are corrupted by a quantization noise. When the number of measurements is not sufficiently large, different $k$-sparse solutions may be present in the feasible set, and the classical l1 approach may be unsuccessful. For this motivation, we propose a non-convex quadratic programming method, which exploits prior information on the magnitude of the non-zero parameters. This results in a more efficient support recovery. We provide sufficient conditions for successful recovery and numerical simulations to illustrate the practical feasibility of the proposed method.