Sparse $\ell_1$ and $\ell_2$ Center Classifiers
Paper and Code
Nov 25, 2019
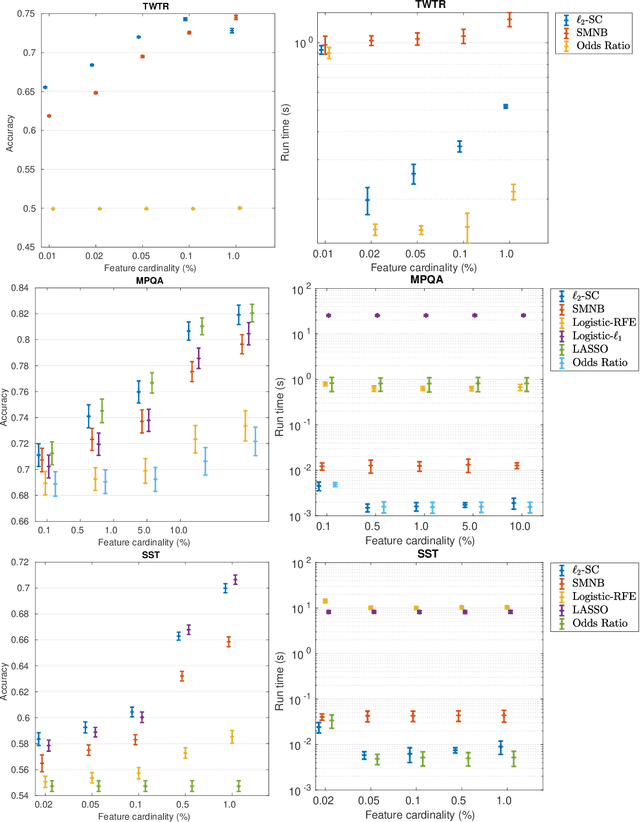

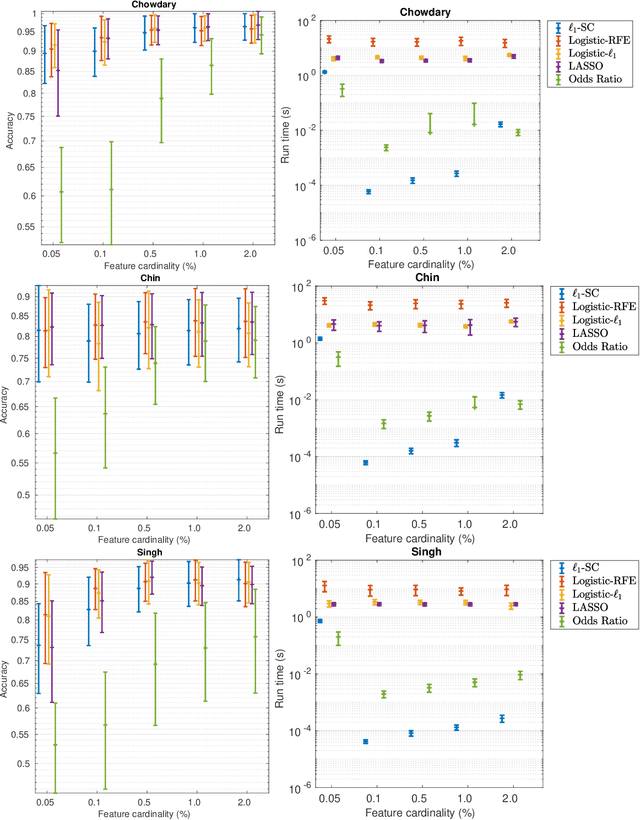
The nearest-centroid classifier is a simple linear-time classifier based on computing the centroids of the data classes in the training phase, and then assigning a new datum to the class corresponding to its nearest centroid. Thanks to its very low computational cost, the nearest-centroid classifier is still widely used in machine learning, despite the development of many other more sophisticated classification methods. In this paper, we propose two sparse variants of the nearest-centroid classifier, based respectively on $\ell_1$ and $\ell_2$ distance criteria. The proposed sparse classifiers perform simultaneous classification and feature selection, by detecting the features that are most relevant for the classification purpose. We show that training of the proposed sparse models, with both distance criteria, can be performed exactly (i.e., the globally optimal set of features is selected) and at a quasi-linear computational cost. The experimental results show that the proposed methods are competitive in accuracy with state-of-the-art feature selection techniques, while having a significantly lower computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge