Reachability analysis in stochastic directed graphs by reinforcement learning
Paper and Code
Feb 25, 2022
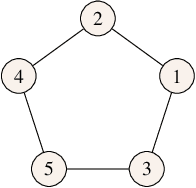

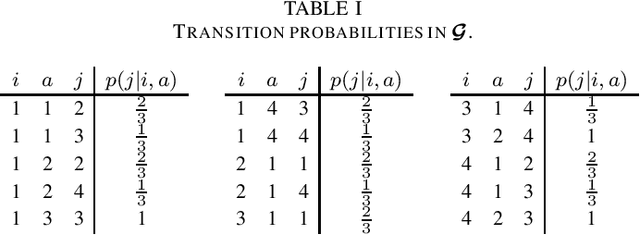
We characterize the reachability probabilities in stochastic directed graphs by means of reinforcement learning methods. In particular, we show that the dynamics of the transition probabilities in a stochastic digraph can be modeled via a difference inclusion, which, in turn, can be interpreted as a Markov decision process. Using the latter framework, we offer a methodology to design reward functions to provide upper and lower bounds on the reachability probabilities of a set of nodes for stochastic digraphs. The effectiveness of the proposed technique is demonstrated by application to the diffusion of epidemic diseases over time-varying contact networks generated by the proximity patterns of mobile agents.
* in IEEE Transactions on Automatic Control, 2023
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge