Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants

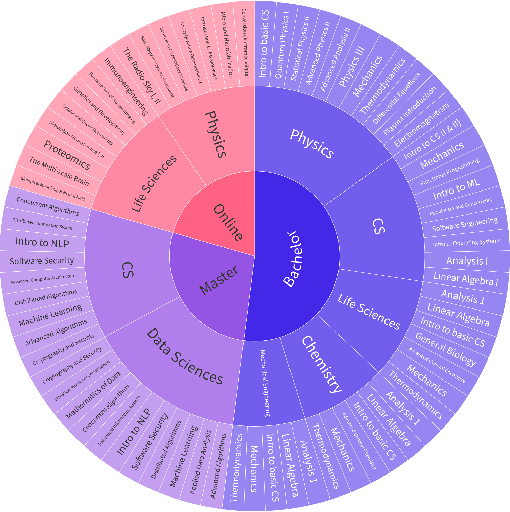
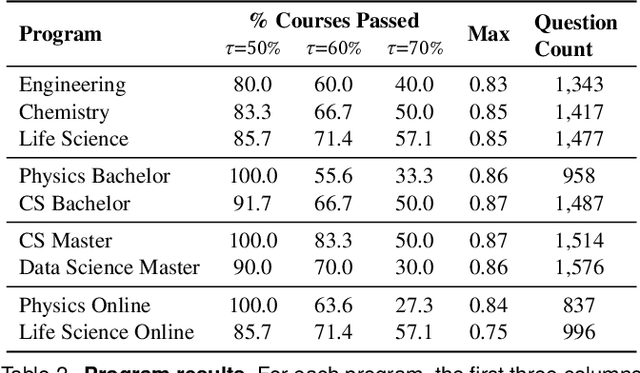
AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.

Efficient algorithms for regularized Poisson Non-negative Matrix Factorization

We consider the problem of regularized Poisson Non-negative Matrix Factorization (NMF) problem, encompassing various regularization terms such as Lipschitz and relatively smooth functions, alongside linear constraints. This problem holds significant relevance in numerous Machine Learning applications, particularly within the domain of physical linear unmixing problems. A notable challenge arises from the main loss term in the Poisson NMF problem being a KL divergence, which is non-Lipschitz, rendering traditional gradient descent-based approaches inefficient. In this contribution, we explore the utilization of Block Successive Upper Minimization (BSUM) to overcome this challenge. We build approriate majorizing function for Lipschitz and relatively smooth functions, and show how to introduce linear constraints into the problem. This results in the development of two novel algorithms for regularized Poisson NMF. We conduct numerical simulations to showcase the effectiveness of our approach.