Beyond the Norms: Detecting Prediction Errors in Regression Models

This paper tackles the challenge of detecting unreliable behavior in regression algorithms, which may arise from intrinsic variability (e.g., aleatoric uncertainty) or modeling errors (e.g., model uncertainty). First, we formally introduce the notion of unreliability in regression, i.e., when the output of the regressor exceeds a specified discrepancy (or error). Then, using powerful tools for probabilistic modeling, we estimate the discrepancy density, and we measure its statistical diversity using our proposed metric for statistical dissimilarity. In turn, this allows us to derive a data-driven score that expresses the uncertainty of the regression outcome. We show empirical improvements in error detection for multiple regression tasks, consistently outperforming popular baseline approaches, and contributing to the broader field of uncertainty quantification and safe machine learning systems. Our code is available at https://zenodo.org/records/11281964.

Classification of sums of complex exponentials

Numerous signals in relevant signal processing applications can be modeled as a sum of complex exponentials. Each exponential term entails a particular property of the modeled physical system, and it is possible to define families of signals that are associated with the complex exponentials. In this paper, we formulate a classification problem for this guiding principle and we propose a data processing strategy. In particular, we exploit the information obtained from the analytical model by combining it with data-driven learning techniques. As a result, we obtain a classification strategy that is robust under modeling uncertainties and experimental perturbations. To assess the performance of the new scheme, we test it with experimental data obtained from the scattering response of targets illuminated with an impulse radio ultra-wideband radar.

On the Correlation between the Noise and a Priori Error Vectors in Affine Projection Algorithms

This paper analyzes the correlation matrix between the a priori error and measurement noise vectors for affine projection algorithms (APA). This correlation stems from the dependence between the filter tap estimates and the noise samples, and has a strong influence on the mean square behavior of the algorithm. We show that the correlation matrix is upper triangular, and compute the diagonal elements in closed form, showing that they are independent of the input process statistics. Also, for white inputs we show that the matrix is fully diagonal. These results are valid in the transient and steady states of the algorithm considering a possibly variable step-size. Our only assumption is that the filter order is large compared to the projection order of APA and we make no assumptions on the input signal except for stationarity. Using these results, we perform a steady-state analysis of the algorithm for small step size and provide a new simple closed-form expression for mean-square error, which has comparable or better accuracy to many preexisting expressions, and is much simpler to compute. Finally, we also obtain expressions for the steady-state energy of the other components of the error vector.

A Time-domain Approach to the Design of Coupled-Resonator Microstrip Filters

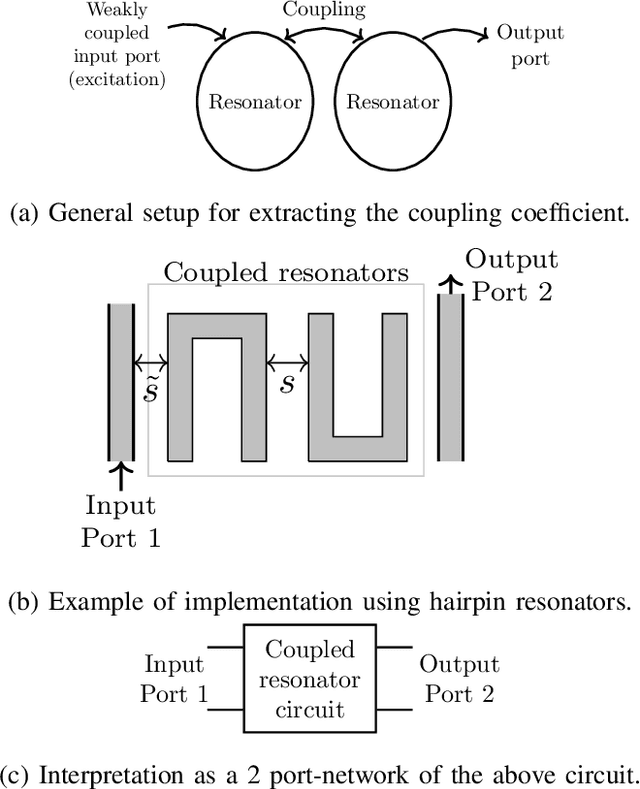
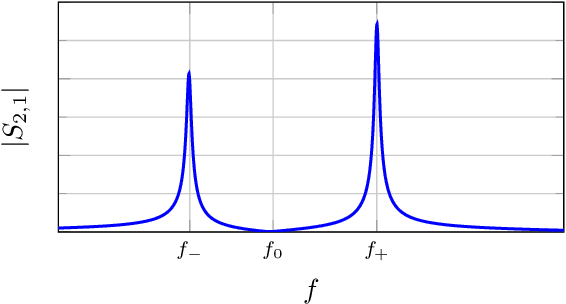
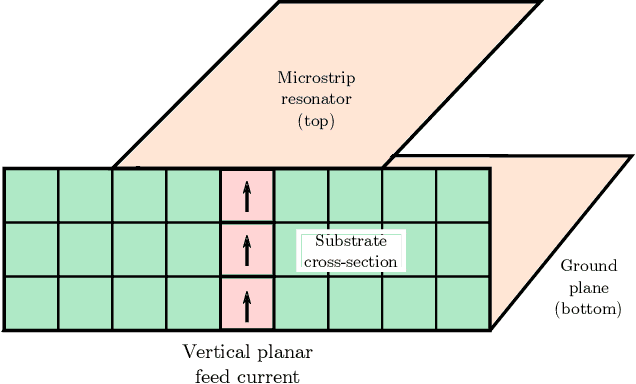
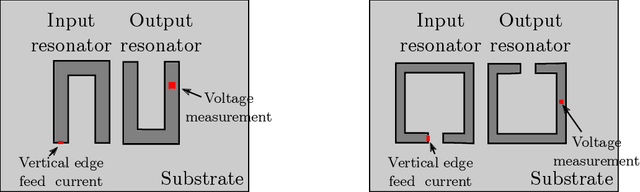
Coupled-resonator microstrip filters are among the most versatile filter topologies. A known design approach uses full-wave electromagnetic simulations to determine the coupling coefficient between resonators as a function of their relative position. This could be done using time-domain simulations using a fast Fourier transform (FFT) to extract the couplings from the S parameters obtained from time-domain signals. However, this approach has a poor performance in terms of resolution and specially for weak couplings, leading to unreasonably long simulation times. To overcome this, we introduce a technique to obtain the couplings directly from time signals, without moving to the frequency domain. This procedure works for strong and weak couplings, with much shorter simulation times and a reduced simulation domain over the FFT approach. This technique is used to design coupled resonator filter efficiently from time domain simulations. We implement this procedure using the finite-difference time-domain framework using an open source solver and discuss our implementation. We show that its results are very similar to previously published ones obtained from frequency domain simulations, even in the case of very weak couplings. Finally, we design and measure a filter to show the good performance of the proposed approach.