Survey schemes for stochastic gradient descent with applications to M-estimation
Paper and Code
Jan 09, 2015
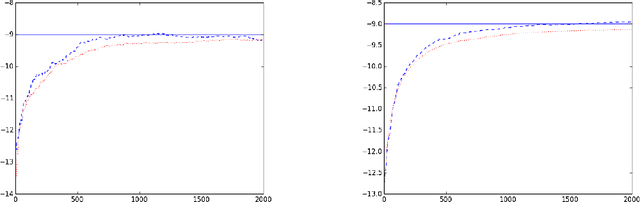
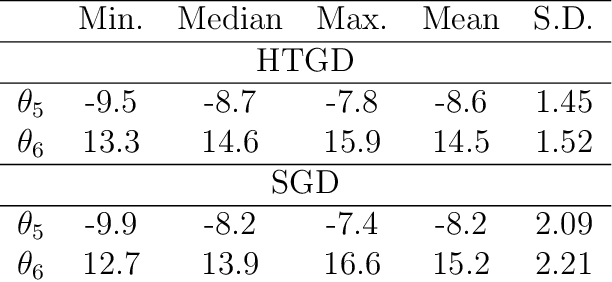
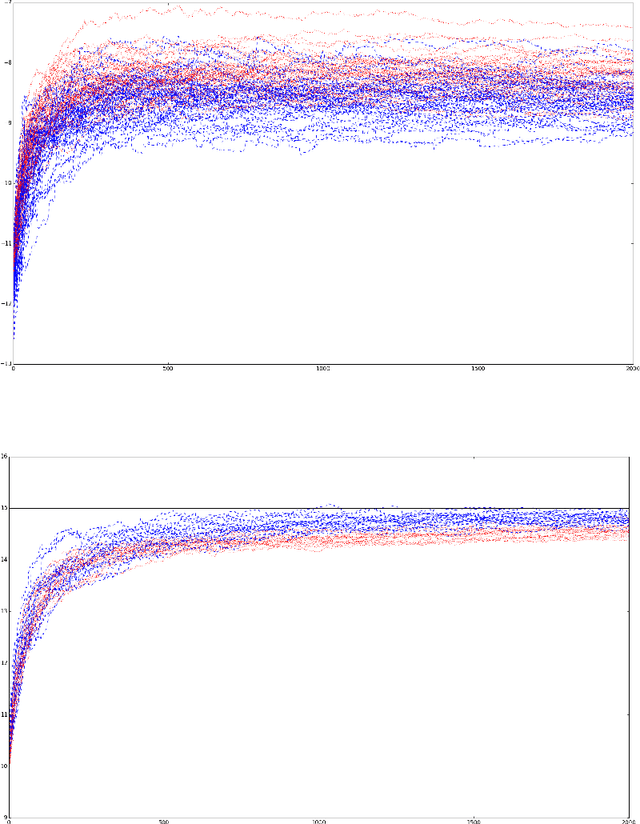
In certain situations that shall be undoubtedly more and more common in the Big Data era, the datasets available are so massive that computing statistics over the full sample is hardly feasible, if not unfeasible. A natural approach in this context consists in using survey schemes and substituting the "full data" statistics with their counterparts based on the resulting random samples, of manageable size. It is the main purpose of this paper to investigate the impact of survey sampling with unequal inclusion probabilities on stochastic gradient descent-based M-estimation methods in large-scale statistical and machine-learning problems. Precisely, we prove that, in presence of some a priori information, one may significantly increase asymptotic accuracy when choosing appropriate first order inclusion probabilities, without affecting complexity. These striking results are described here by limit theorems and are also illustrated by numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge