Individual Survival Curves with Conditional Normalizing Flows
Paper and Code
Jul 27, 2021
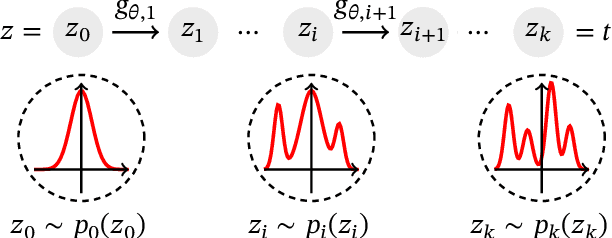
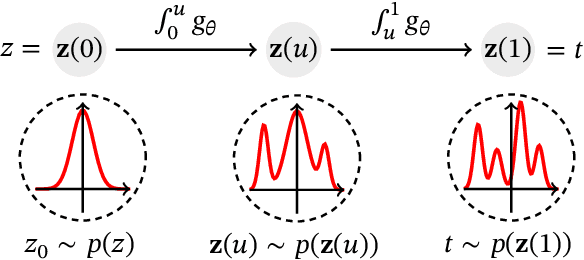

Survival analysis, or time-to-event modelling, is a classical statistical problem that has garnered a lot of interest for its practical use in epidemiology, demographics or actuarial sciences. Recent advances on the subject from the point of view of machine learning have been concerned with precise per-individual predictions instead of population studies, driven by the rise of individualized medicine. We introduce here a conditional normalizing flow based estimate of the time-to-event density as a way to model highly flexible and individualized conditional survival distributions. We use a novel hierarchical formulation of normalizing flows to enable efficient fitting of flexible conditional distributions without overfitting and show how the normalizing flow formulation can be efficiently adapted to the censored setting. We experimentally validate the proposed approach on a synthetic dataset as well as four open medical datasets and an example of a common financial problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge