Functional Anomaly Detection: a Benchmark Study

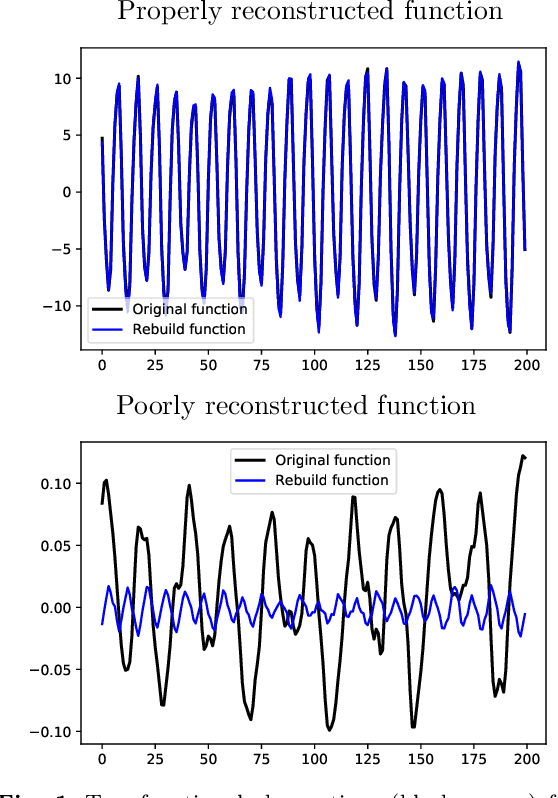
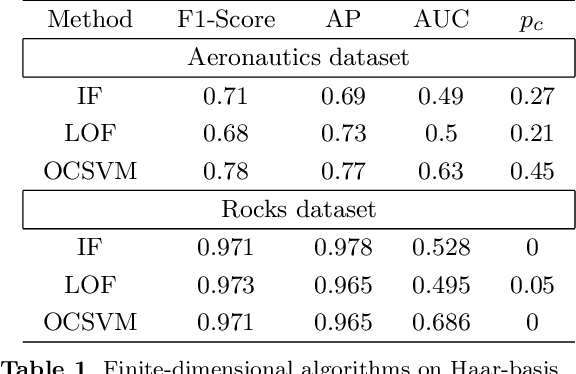
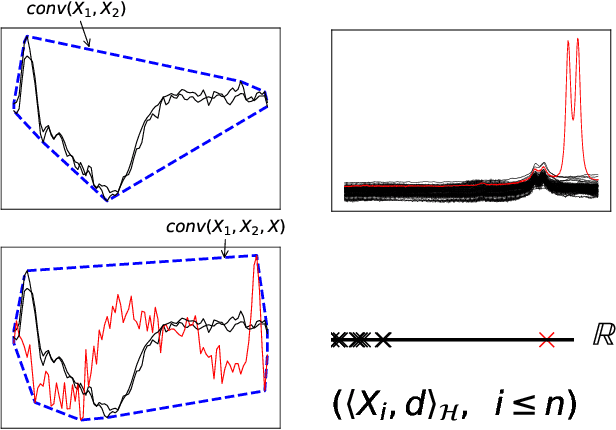
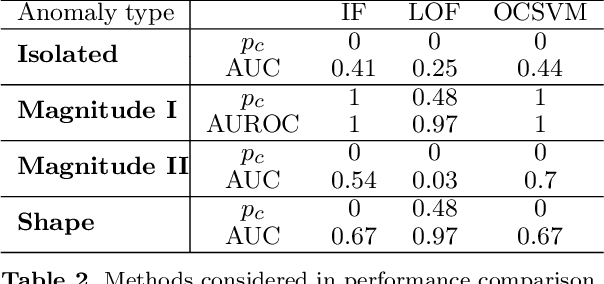
The increasing automation in many areas of the Industry expressly demands to design efficient machine-learning solutions for the detection of abnormal events. With the ubiquitous deployment of sensors monitoring nearly continuously the health of complex infrastructures, anomaly detection can now rely on measurements sampled at a very high frequency, providing a very rich representation of the phenomenon under surveillance. In order to exploit fully the information thus collected, the observations cannot be treated as multivariate data anymore and a functional analysis approach is required. It is the purpose of this paper to investigate the performance of recent techniques for anomaly detection in the functional setup on real datasets. After an overview of the state-of-the-art and a visual-descriptive study, a variety of anomaly detection methods are compared. While taxonomies of abnormalities (e.g. shape, location) in the functional setup are documented in the literature, assigning a specific type to the identified anomalies appears to be a challenging task. Thus, strengths and weaknesses of the existing approaches are benchmarked in view of these highlighted types in a simulation study. Anomaly detection methods are next evaluated on two datasets, related to the monitoring of helicopters in flight and to the spectrometry of construction materials namely. The benchmark analysis is concluded by recommendation guidance for practitioners.

Kalman Recursions Aggregated Online

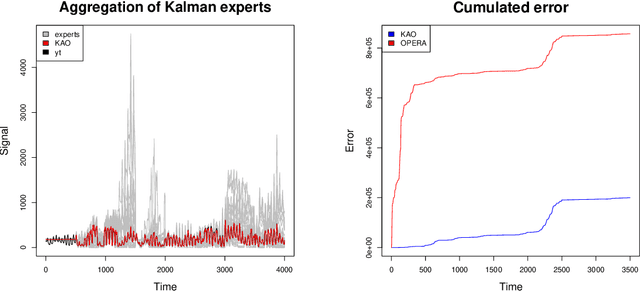
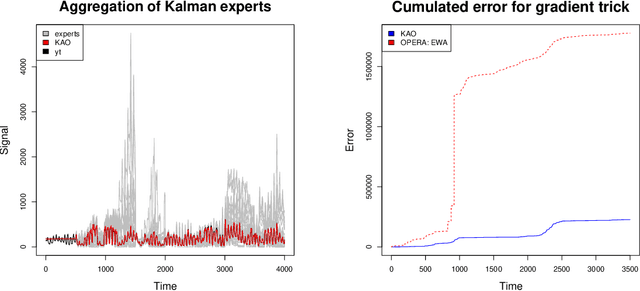
In this article, we aim at improving the prediction of expert aggregation by using the underlying properties of the models that provide expert predictions. We restrict ourselves to the case where expert predictions come from Kalman recursions, fitting state-space models. By using exponential weights, we construct different algorithms of Kalman recursions Aggregated Online (KAO) that compete with the best expert or the best convex combination of experts in a more or less adaptive way. We improve the existing results on expert aggregation literature when the experts are Kalman recursions by taking advantage of the second-order properties of the Kalman recursions. We apply our approach to Kalman recursions and extend it to the general adversarial expert setting by state-space modeling the errors of the experts. We apply these new algorithms to a real dataset of electricity consumption and show how it can improve forecast performances comparing to other exponentially weighted average procedures.