Shirshendu Chatterjee
Concentration inequalities for correlated network-valued processes with applications to community estimation and changepoint analysis
Aug 02, 2022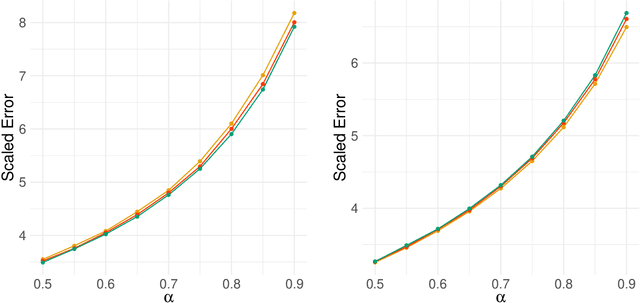
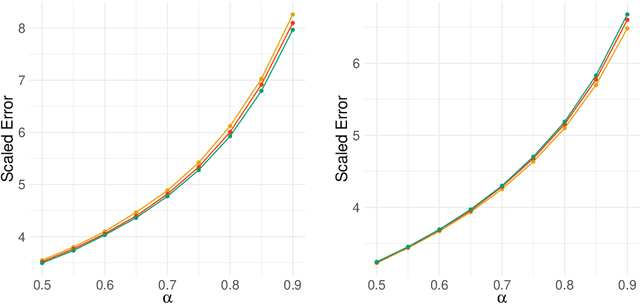
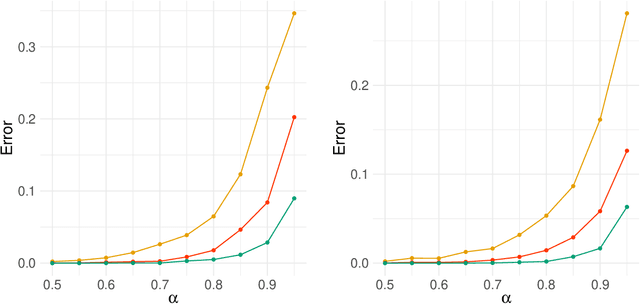

Abstract:Network-valued time series are currently a common form of network data. However, the study of the aggregate behavior of network sequences generated from network-valued stochastic processes is relatively rare. Most of the existing research focuses on the simple setup where the networks are independent (or conditionally independent) across time, and all edges are updated synchronously at each time step. In this paper, we study the concentration properties of the aggregated adjacency matrix and the corresponding Laplacian matrix associated with network sequences generated from lazy network-valued stochastic processes, where edges update asynchronously, and each edge follows a lazy stochastic process for its updates independent of the other edges. We demonstrate the usefulness of these concentration results in proving consistency of standard estimators in community estimation and changepoint estimation problems. We also conduct a simulation study to demonstrate the effect of the laziness parameter, which controls the extent of temporal correlation, on the accuracy of community and changepoint estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge