Concentration inequalities for correlated network-valued processes with applications to community estimation and changepoint analysis

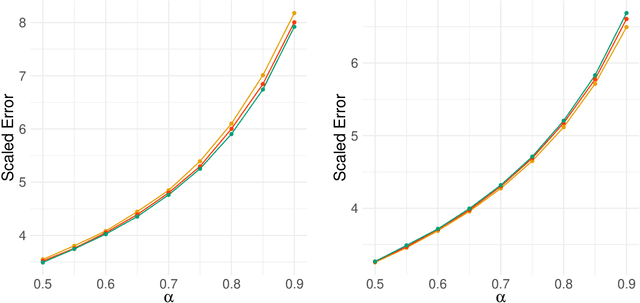
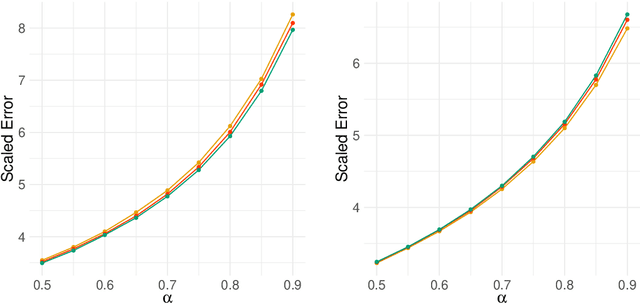
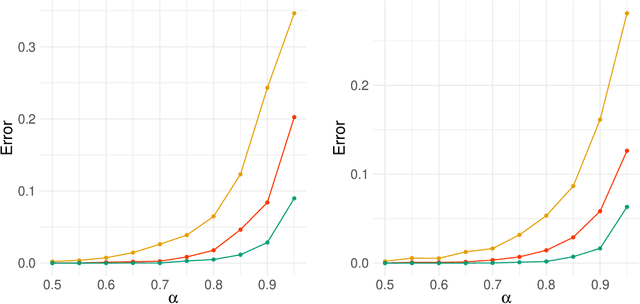
Network-valued time series are currently a common form of network data. However, the study of the aggregate behavior of network sequences generated from network-valued stochastic processes is relatively rare. Most of the existing research focuses on the simple setup where the networks are independent (or conditionally independent) across time, and all edges are updated synchronously at each time step. In this paper, we study the concentration properties of the aggregated adjacency matrix and the corresponding Laplacian matrix associated with network sequences generated from lazy network-valued stochastic processes, where edges update asynchronously, and each edge follows a lazy stochastic process for its updates independent of the other edges. We demonstrate the usefulness of these concentration results in proving consistency of standard estimators in community estimation and changepoint estimation problems. We also conduct a simulation study to demonstrate the effect of the laziness parameter, which controls the extent of temporal correlation, on the accuracy of community and changepoint estimation.

Hierarchical community detection by recursive bi-partitioning

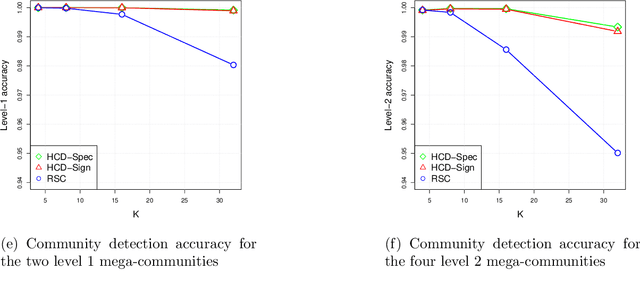
The problem of community detection in networks is usually formulated as finding a single partition of the network into some "correct" number of communities. We argue that it is more interpretable and in some regimes more accurate to construct a hierarchical tree of communities instead. This can be done with a simple top-down recursive bi-partitioning algorithm, starting with a single community and separating the nodes into two communities by spectral clustering repeatedly, until a stopping rule suggests there are no further communities. Such an algorithm is model-free, extremely fast, and requires no tuning other than selecting a stopping rule. We show that there are regimes where it outperforms $K$-way spectral clustering, and propose a natural model for analyzing the algorithm's theoretical performance, the binary tree stochastic block model. Under this model, we prove that the algorithm correctly recovers the entire community tree under relatively mild assumptions. We also apply the algorithm to a dataset of statistics papers to construct a hierarchical tree of statistical research communities.

Optimizing the Union of Intersections LASSO ($UoI_{LASSO}$) and Vector Autoregressive ($UoI_{VAR}$) Algorithms for Improved Statistical Estimation at Scale

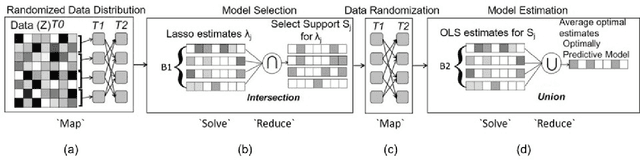
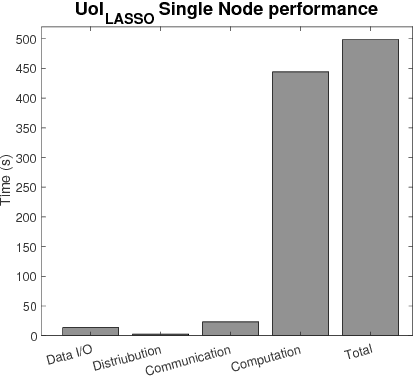
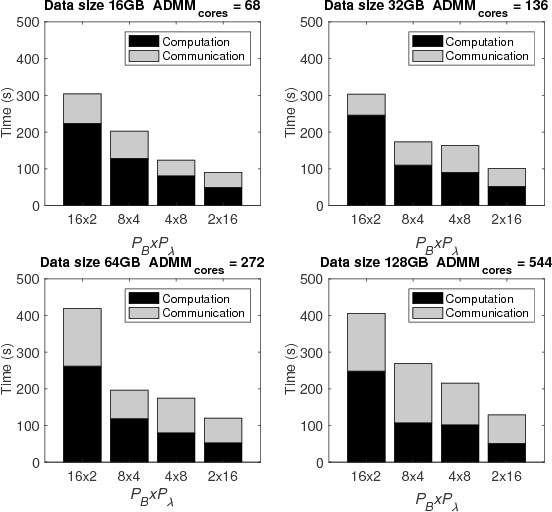
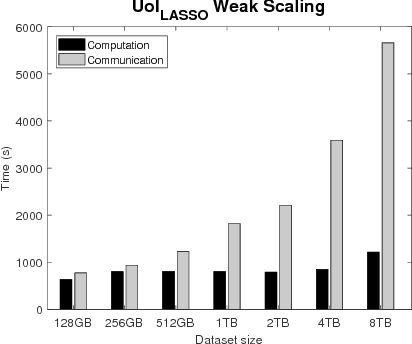
The analysis of scientific data of increasing size and complexity requires statistical machine learning methods that are both interpretable and predictive. Union of Intersections (UoI), a recently developed framework, is a two-step approach that separates model selection and model estimation. A linear regression algorithm based on UoI, $UoI_{LASSO}$, simultaneously achieves low false positives and low false negative feature selection as well as low bias and low variance estimates. Together, these qualities make the results both predictive and interpretable. In this paper, we optimize the $UoI_{LASSO}$ algorithm for single-node execution on NERSC's Cori Knights Landing, a Xeon Phi based supercomputer. We then scale $UoI_{LASSO}$ to execute on cores ranging from 68-278,528 cores on a range of dataset sizes demonstrating the weak and strong scaling of the implementation. We also implement a variant of $UoI_{LASSO}$, $UoI_{VAR}$ for vector autoregressive models, to analyze high dimensional time-series data. We perform single node optimization and multi-node scaling experiments for $UoI_{VAR}$ to demonstrate the effectiveness of the algorithm for weak and strong scaling. Our implementations enable to use estimate the largest VAR model (1000 nodes) we are aware of, and apply it to large neurophysiology data 192 nodes).

Union of Intersections (UoI) for Interpretable Data Driven Discovery and Prediction

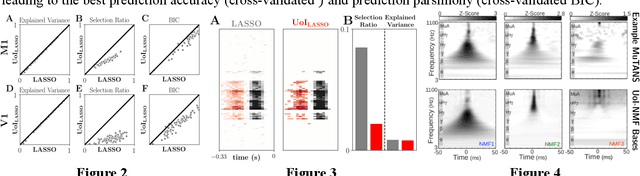
The increasing size and complexity of scientific data could dramatically enhance discovery and prediction for basic scientific applications. Realizing this potential, however, requires novel statistical analysis methods that are both interpretable and predictive. We introduce Union of Intersections (UoI), a flexible, modular, and scalable framework for enhanced model selection and estimation. Methods based on UoI perform model selection and model estimation through intersection and union operations, respectively. We show that UoI-based methods achieve low-variance and nearly unbiased estimation of a small number of interpretable features, while maintaining high-quality prediction accuracy. We perform extensive numerical investigation to evaluate a UoI algorithm ($UoI_{Lasso}$) on synthetic and real data. In doing so, we demonstrate the extraction of interpretable functional networks from human electrophysiology recordings as well as accurate prediction of phenotypes from genotype-phenotype data with reduced features. We also show (with the $UoI_{L1Logistic}$ and $UoI_{CUR}$ variants of the basic framework) improved prediction parsimony for classification and matrix factorization on several benchmark biomedical data sets. These results suggest that methods based on the UoI framework could improve interpretation and prediction in data-driven discovery across scientific fields.

Spectral Clustering and Block Models: A Review And A New Algorithm

We focus on spectral clustering of unlabeled graphs and review some results on clustering methods which achieve weak or strong consistent identification in data generated by such models. We also present a new algorithm which appears to perform optimally both theoretically using asymptotic theory and empirically.

Community Detection in Networks using Graph Distance

The study of networks has received increased attention recently not only from the social sciences and statistics but also from physicists, computer scientists and mathematicians. One of the principal problem in networks is community detection. Many algorithms have been proposed for community finding but most of them do not have have theoretical guarantee for sparse networks and networks close to the phase transition boundary proposed by physicists. There are some exceptions but all have some incomplete theoretical basis. Here we propose an algorithm based on the graph distance of vertices in the network. We give theoretical guarantees that our method works in identifying communities for block models and can be extended for degree-corrected block models and block models with the number of communities growing with number of vertices. Despite favorable simulation results, we are not yet able to conclude that our method is satisfactory for worst possible case. We illustrate on a network of political blogs, Facebook networks and some other networks.