Learning from learning machines: a new generation of AI technology to meet the needs of science

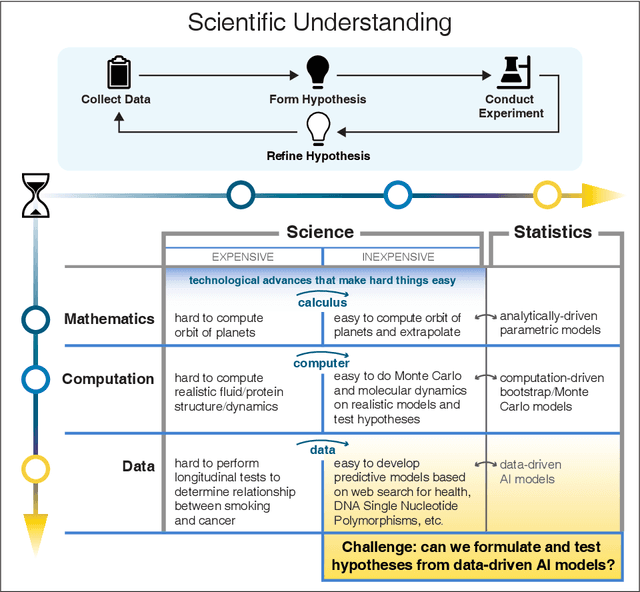
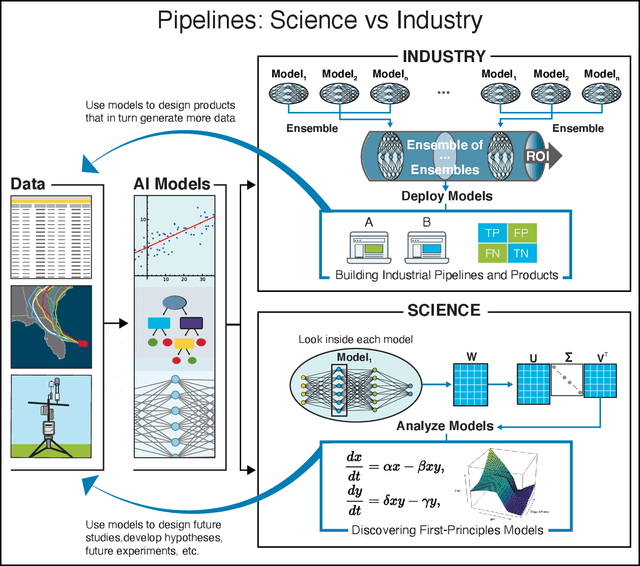
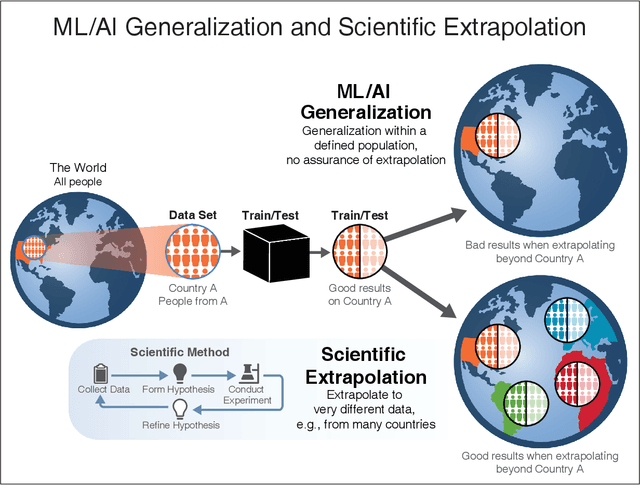
We outline emerging opportunities and challenges to enhance the utility of AI for scientific discovery. The distinct goals of AI for industry versus the goals of AI for science create tension between identifying patterns in data versus discovering patterns in the world from data. If we address the fundamental challenges associated with "bridging the gap" between domain-driven scientific models and data-driven AI learning machines, then we expect that these AI models can transform hypothesis generation, scientific discovery, and the scientific process itself.

Sparse Canonical Correlation Analysis via Concave Minimization

A new approach to the sparse Canonical Correlation Analysis (sCCA)is proposed with the aim of discovering interpretable associations in very high-dimensional multi-view, i.e.observations of multiple sets of variables on the same subjects, problems. Inspired by the sparse PCA approach of Journee et al. (2010), we also show that the sparse CCA formulation, while non-convex, is equivalent to a maximization program of a convex objective over a compact set for which we propose a first-order gradient method. This result helps us reduce the search space drastically to the boundaries of the set. Consequently, we propose a two-step algorithm, where we first infer the sparsity pattern of the canonical directions using our fast algorithm, then we shrink each view, i.e. observations of a set of covariates, to contain observations on the sets of covariates selected in the previous step, and compute their canonical directions via any CCA algorithm. We also introduceDirected Sparse CCA, which is able to find associations which are aligned with a specified experiment design, andMulti-View sCCA which is used to discover associations between multiple sets of covariates. Our simulations establish the superior convergence properties and computational efficiency of our algorithm as well as accuracy in terms of the canonical correlation and its ability to recover the supports of the canonical directions. We study the associations between metabolomics, trasncriptomics and microbiomics in a multi-omic study usingMuLe, which is an R-package that implements our approach, in order to form hypotheses on mechanisms of adaptations of Drosophila Melanogaster to high doses of environmental toxicants, specifically Atrazine, which is a commonly used chemical fertilizer.

Hierarchical community detection by recursive bi-partitioning

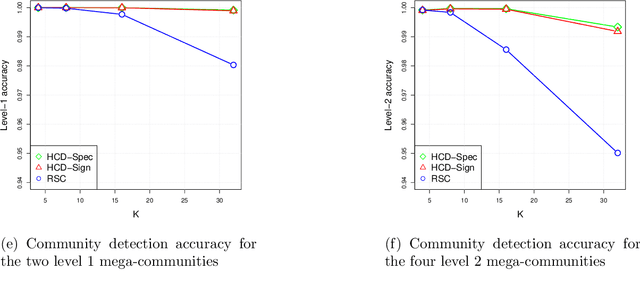
The problem of community detection in networks is usually formulated as finding a single partition of the network into some "correct" number of communities. We argue that it is more interpretable and in some regimes more accurate to construct a hierarchical tree of communities instead. This can be done with a simple top-down recursive bi-partitioning algorithm, starting with a single community and separating the nodes into two communities by spectral clustering repeatedly, until a stopping rule suggests there are no further communities. Such an algorithm is model-free, extremely fast, and requires no tuning other than selecting a stopping rule. We show that there are regimes where it outperforms $K$-way spectral clustering, and propose a natural model for analyzing the algorithm's theoretical performance, the binary tree stochastic block model. Under this model, we prove that the algorithm correctly recovers the entire community tree under relatively mild assumptions. We also apply the algorithm to a dataset of statistics papers to construct a hierarchical tree of statistical research communities.

Two provably consistent divide and conquer clustering algorithms for large networks

In this article, we advance divide-and-conquer strategies for solving the community detection problem in networks. We propose two algorithms which perform clustering on a number of small subgraphs and finally patches the results into a single clustering. The main advantage of these algorithms is that they bring down significantly the computational cost of traditional algorithms, including spectral clustering, semi-definite programs, modularity based methods, likelihood based methods etc., without losing on accuracy and even improving accuracy at times. These algorithms are also, by nature, parallelizable. Thus, exploiting the facts that most traditional algorithms are accurate and the corresponding optimization problems are much simpler in small problems, our divide-and-conquer methods provide an omnibus recipe for scaling traditional algorithms up to large networks. We prove consistency of these algorithms under various subgraph selection procedures and perform extensive simulations and real-data analysis to understand the advantages of the divide-and-conquer approach in various settings.

Spectral Clustering and Block Models: A Review And A New Algorithm

We focus on spectral clustering of unlabeled graphs and review some results on clustering methods which achieve weak or strong consistent identification in data generated by such models. We also present a new algorithm which appears to perform optimally both theoretically using asymptotic theory and empirically.

Role of normalization in spectral clustering for stochastic blockmodels

Spectral clustering is a technique that clusters elements using the top few eigenvectors of their (possibly normalized) similarity matrix. The quality of spectral clustering is closely tied to the convergence properties of these principal eigenvectors. This rate of convergence has been shown to be identical for both the normalized and unnormalized variants in recent random matrix theory literature. However, normalization for spectral clustering is commonly believed to be beneficial [Stat. Comput. 17 (2007) 395-416]. Indeed, our experiments show that normalization improves prediction accuracy. In this paper, for the popular stochastic blockmodel, we theoretically show that normalization shrinks the spread of points in a class by a constant fraction under a broad parameter regime. As a byproduct of our work, we also obtain sharp deviation bounds of empirical principal eigenvalues of graphs generated from a stochastic blockmodel.

Community Detection in Networks using Graph Distance

The study of networks has received increased attention recently not only from the social sciences and statistics but also from physicists, computer scientists and mathematicians. One of the principal problem in networks is community detection. Many algorithms have been proposed for community finding but most of them do not have have theoretical guarantee for sparse networks and networks close to the phase transition boundary proposed by physicists. There are some exceptions but all have some incomplete theoretical basis. Here we propose an algorithm based on the graph distance of vertices in the network. We give theoretical guarantees that our method works in identifying communities for block models and can be extended for degree-corrected block models and block models with the number of communities growing with number of vertices. Despite favorable simulation results, we are not yet able to conclude that our method is satisfactory for worst possible case. We illustrate on a network of political blogs, Facebook networks and some other networks.

Hypothesis Testing for Automated Community Detection in Networks

Community detection in networks is a key exploratory tool with applications in a diverse set of areas, ranging from finding communities in social and biological networks to identifying link farms in the World Wide Web. The problem of finding communities or clusters in a network has received much attention from statistics, physics and computer science. However, most clustering algorithms assume knowledge of the number of clusters k. In this paper we propose to automatically determine k in a graph generated from a Stochastic Blockmodel. Our main contribution is twofold; first, we theoretically establish the limiting distribution of the principal eigenvalue of the suitably centered and scaled adjacency matrix, and use that distribution for our hypothesis test. Secondly, we use this test to design a recursive bipartitioning algorithm. Using quantifiable classification tasks on real world networks with ground truth, we show that our algorithm outperforms existing probabilistic models for learning overlapping clusters, and on unlabeled networks, we show that we uncover nested community structure.

Pseudo-likelihood methods for community detection in large sparse networks

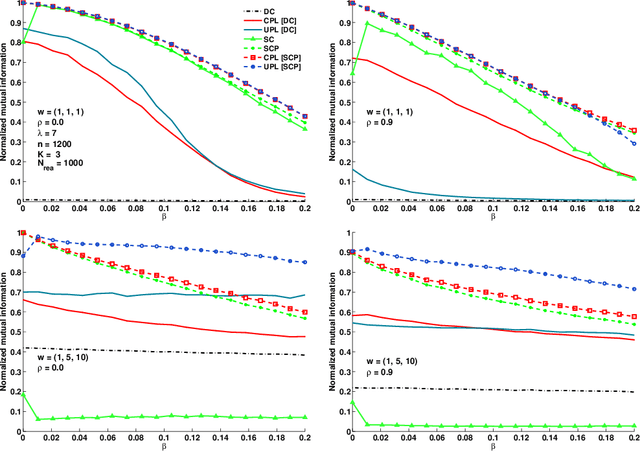
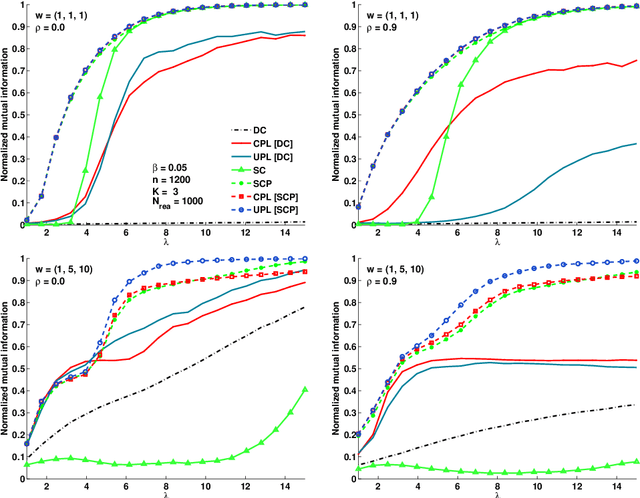
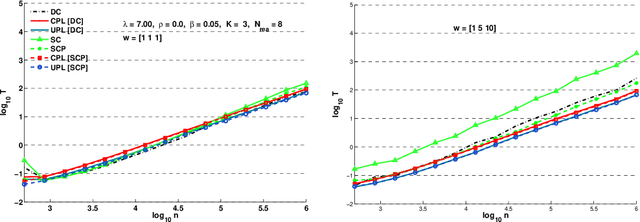
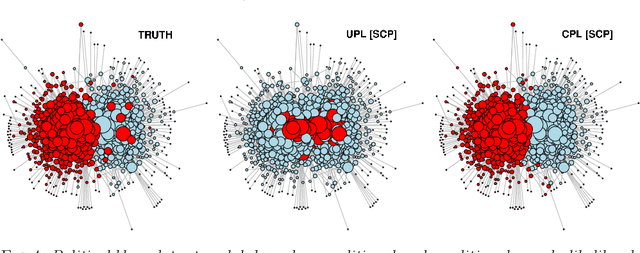
Many algorithms have been proposed for fitting network models with communities, but most of them do not scale well to large networks, and often fail on sparse networks. Here we propose a new fast pseudo-likelihood method for fitting the stochastic block model for networks, as well as a variant that allows for an arbitrary degree distribution by conditioning on degrees. We show that the algorithms perform well under a range of settings, including on very sparse networks, and illustrate on the example of a network of political blogs. We also propose spectral clustering with perturbations, a method of independent interest, which works well on sparse networks where regular spectral clustering fails, and use it to provide an initial value for pseudo-likelihood. We prove that pseudo-likelihood provides consistent estimates of the communities under a mild condition on the starting value, for the case of a block model with two communities.

Large Vector Auto Regressions

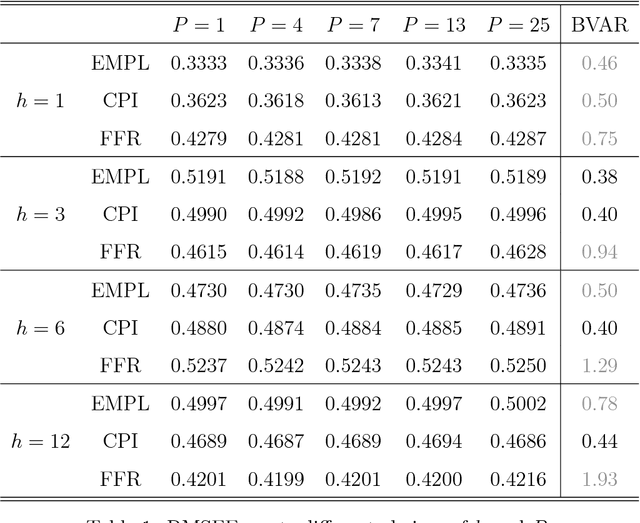
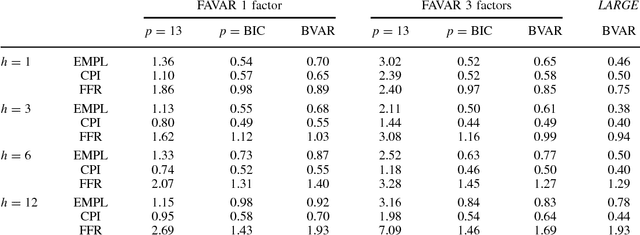
One popular approach for nonstructural economic and financial forecasting is to include a large number of economic and financial variables, which has been shown to lead to significant improvements for forecasting, for example, by the dynamic factor models. A challenging issue is to determine which variables and (their) lags are relevant, especially when there is a mixture of serial correlation (temporal dynamics), high dimensional (spatial) dependence structure and moderate sample size (relative to dimensionality and lags). To this end, an \textit{integrated} solution that addresses these three challenges simultaneously is appealing. We study the large vector auto regressions here with three types of estimates. We treat each variable's own lags different from other variables' lags, distinguish various lags over time, and is able to select the variables and lags simultaneously. We first show the consequences of using Lasso type estimate directly for time series without considering the temporal dependence. In contrast, our proposed method can still produce an estimate as efficient as an \textit{oracle} under such scenarios. The tuning parameters are chosen via a data driven "rolling scheme" method to optimize the forecasting performance. A macroeconomic and financial forecasting problem is considered to illustrate its superiority over existing estimators.