Uni-RXN: A Unified Framework Bridging the Gap between Chemical Reaction Pretraining and Conditional Molecule Generation

Chemical reactions are the fundamental building blocks of drug design and organic chemistry research. In recent years, there has been a growing need for a large-scale deep-learning framework that can efficiently capture the basic rules of chemical reactions. In this paper, we have proposed a unified framework that addresses both the reaction representation learning and molecule generation tasks, which allows for a more holistic approach. Inspired by the organic chemistry mechanism, we develop a novel pretraining framework that enables us to incorporate inductive biases into the model. Our framework achieves state-of-the-art results on challenging downstream tasks. By possessing chemical knowledge, this framework can be applied to reaction-based generative models, overcoming the limitations of current molecule generation models that rely on a small number of reaction templates. In the extensive experiments, our model generates synthesizable drug-like structures of high quality. Overall, our work presents a significant step toward a large-scale deep-learning framework for a variety of reaction-based applications.

Dynamic Large Spatial Covariance Matrix Estimation in Application to Semiparametric Model Construction via Variable Clustering: the SCE approach

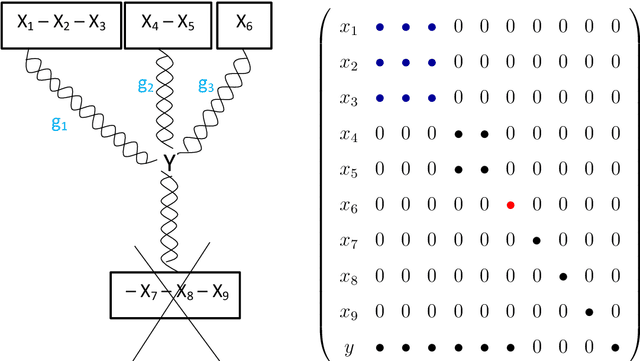
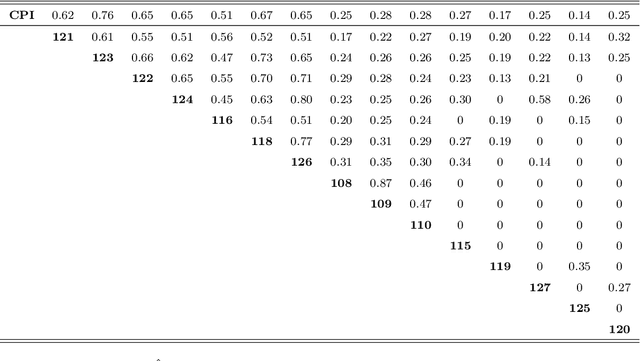
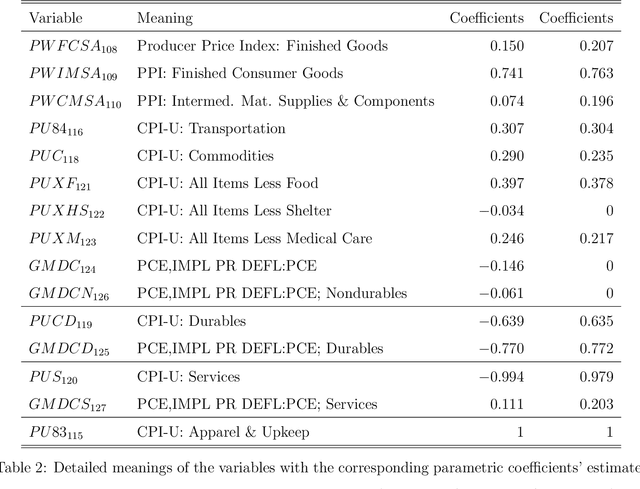
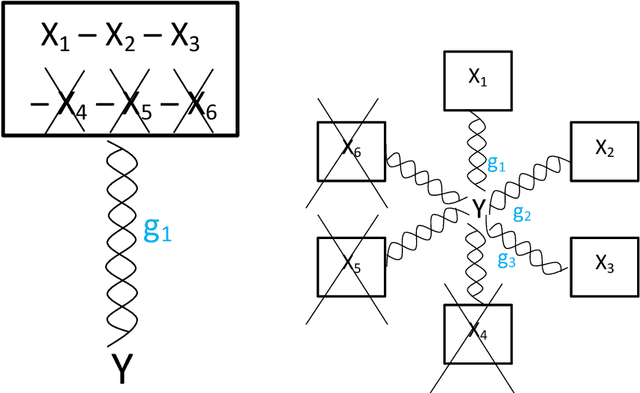
To better understand the spatial structure of large panels of economic and financial time series and provide a guideline for constructing semiparametric models, this paper first considers estimating a large spatial covariance matrix of the generalized $m$-dependent and $\beta$-mixing time series (with $J$ variables and $T$ observations) by hard thresholding regularization as long as ${{\log J \, \cx^*(\ct)}}/{T} = \Co(1)$ (the former scheme with some time dependence measure $\cx^*(\ct)$) or $\log J /{T} = \Co(1)$ (the latter scheme with some upper bounded mixing coefficient). We quantify the interplay between the estimators' consistency rate and the time dependence level, discuss an intuitive resampling scheme for threshold selection, and also prove a general cross-validation result justifying this. Given a consistently estimated covariance (correlation) matrix, by utilizing its natural links with graphical models and semiparametrics, after "screening" the (explanatory) variables, we implement a novel forward (and backward) label permutation procedure to cluster the "relevant" variables and construct the corresponding semiparametric model, which is further estimated by the groupwise dimension reduction method with sign constraints. We call this the SCE (screen - cluster - estimate) approach for modeling high dimensional data with complex spatial structure. Finally we apply this method to study the spatial structure of large panels of economic and financial time series and find the proper semiparametric structure for estimating the consumer price index (CPI) to illustrate its superiority over the linear models.

Large Vector Auto Regressions

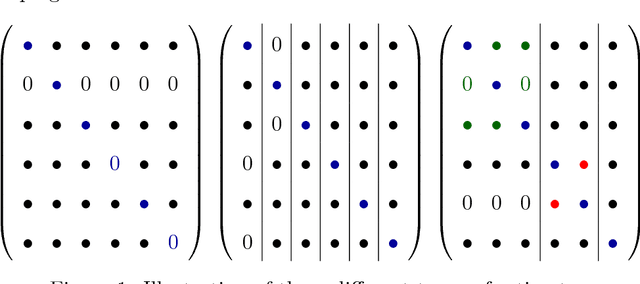
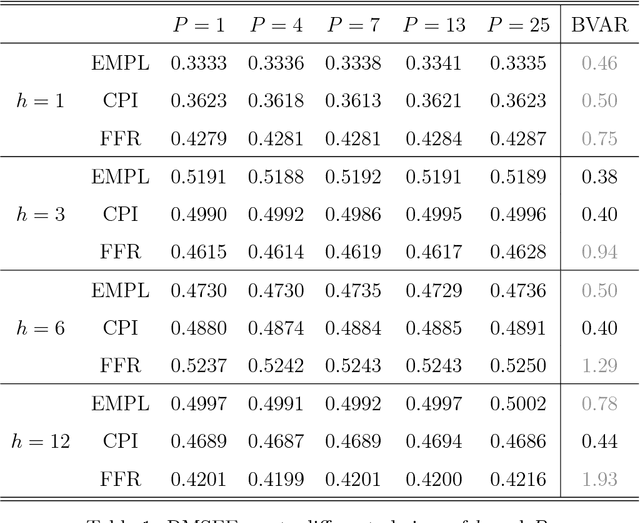
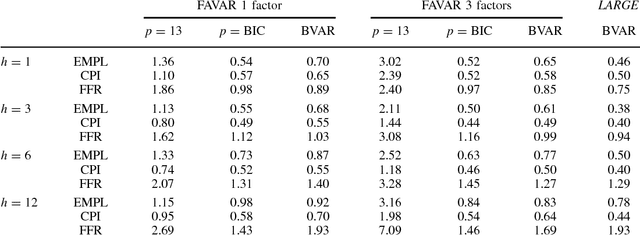
One popular approach for nonstructural economic and financial forecasting is to include a large number of economic and financial variables, which has been shown to lead to significant improvements for forecasting, for example, by the dynamic factor models. A challenging issue is to determine which variables and (their) lags are relevant, especially when there is a mixture of serial correlation (temporal dynamics), high dimensional (spatial) dependence structure and moderate sample size (relative to dimensionality and lags). To this end, an \textit{integrated} solution that addresses these three challenges simultaneously is appealing. We study the large vector auto regressions here with three types of estimates. We treat each variable's own lags different from other variables' lags, distinguish various lags over time, and is able to select the variables and lags simultaneously. We first show the consequences of using Lasso type estimate directly for time series without considering the temporal dependence. In contrast, our proposed method can still produce an estimate as efficient as an \textit{oracle} under such scenarios. The tuning parameters are chosen via a data driven "rolling scheme" method to optimize the forecasting performance. A macroeconomic and financial forecasting problem is considered to illustrate its superiority over existing estimators.