Tianxi Li
Fitting Low-rank Models on Egocentrically Sampled Partial Networks
Mar 09, 2023



Abstract:The statistical modeling of random networks has been widely used to uncover interaction mechanisms in complex systems and to predict unobserved links in real-world networks. In many applications, network connections are collected via egocentric sampling: a subset of nodes is sampled first, after which all links involving this subset are recorded; all other information is missing. Compared with the assumption of ``uniformly missing at random", egocentrically sampled partial networks require specially designed modeling strategies. Current statistical methods are either computationally infeasible or based on intuitive designs without theoretical justification. Here, we propose an approach to fit general low-rank models for egocentrically sampled networks, which include several popular network models. This method is based on graph spectral properties and is computationally efficient for large-scale networks. It results in consistent recovery of missing subnetworks due to egocentric sampling for sparse networks. To our knowledge, this method offers the first theoretical guarantee for egocentric partial network estimation in the scope of low-rank models. We evaluate the technique on several synthetic and real-world networks and show that it delivers competitive performance in link prediction tasks.
The non-overlapping statistical approximation to overlapping group lasso
Nov 16, 2022



Abstract:Group lasso is a commonly used regularization method in statistical learning in which parameters are eliminated from the model according to predefined groups. However, when the groups overlap, optimizing the group lasso penalized objective can be time-consuming on large-scale problems because of the non-separability induced by the overlapping groups. This bottleneck has seriously limited the application of overlapping group lasso regularization in many modern problems, such as gene pathway selection and graphical model estimation. In this paper, we propose a separable penalty as an approximation of the overlapping group lasso penalty. Thanks to the separability, the computation of regularization based on our penalty is substantially faster than that of the overlapping group lasso, especially for large-scale and high-dimensional problems. We show that the penalty is the tightest separable relaxation of the overlapping group lasso norm within the family of $\ell_{q_1}/\ell_{q_2}$ norms. Moreover, we show that the estimator based on the proposed separable penalty is statistically equivalent to the one based on the overlapping group lasso penalty with respect to their error bounds and the rate-optimal performance under the squared loss. We demonstrate the faster computational time and statistical equivalence of our method compared with the overlapping group lasso in simulation examples and a classification problem of cancer tumors based on gene expression and multiple gene pathways.
Incrementality Bidding via Reinforcement Learning under Mixed and Delayed Rewards
Jun 02, 2022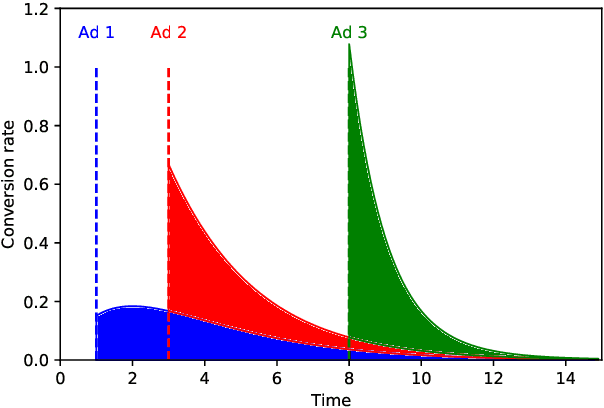
Abstract:Incrementality, which is used to measure the causal effect of showing an ad to a potential customer (e.g. a user in an internet platform) versus not, is a central object for advertisers in online advertising platforms. This paper investigates the problem of how an advertiser can learn to optimize the bidding sequence in an online manner \emph{without} knowing the incrementality parameters in advance. We formulate the offline version of this problem as a specially structured episodic Markov Decision Process (MDP) and then, for its online learning counterpart, propose a novel reinforcement learning (RL) algorithm with regret at most $\widetilde{O}(H^2\sqrt{T})$, which depends on the number of rounds $H$ and number of episodes $T$, but does not depend on the number of actions (i.e., possible bids). A fundamental difference between our learning problem from standard RL problems is that the realized reward feedback from conversion incrementality is \emph{mixed} and \emph{delayed}. To handle this difficulty we propose and analyze a novel pairwise moment-matching algorithm to learn the conversion incrementality, which we believe is of independent of interest.
Diffusion Source Identification on Networks with Statistical Confidence
Jun 17, 2021



Abstract:Diffusion source identification on networks is a problem of fundamental importance in a broad class of applications, including rumor controlling and virus identification. Though this problem has received significant recent attention, most studies have focused only on very restrictive settings and lack theoretical guarantees for more realistic networks. We introduce a statistical framework for the study of diffusion source identification and develop a confidence set inference approach inspired by hypothesis testing. Our method efficiently produces a small subset of nodes, which provably covers the source node with any pre-specified confidence level without restrictive assumptions on network structures. Moreover, we propose multiple Monte Carlo strategies for the inference procedure based on network topology and the probabilistic properties that significantly improve the scalability. To our knowledge, this is the first diffusion source identification method with a practically useful theoretical guarantee on general networks. We demonstrate our approach via extensive synthetic experiments on well-known random network models and a mobility network between cities concerning the COVID-19 spreading.
Network Estimation by Mixing: Adaptivity and More
Jun 05, 2021



Abstract:Networks analysis has been commonly used to study the interactions between units of complex systems. One problem of particular interest is learning the network's underlying connection pattern given a single and noisy instantiation. While many methods have been proposed to address this problem in recent years, they usually assume that the true model belongs to a known class, which is not verifiable in most real-world applications. Consequently, network modeling based on these methods either suffers from model misspecification or relies on additional model selection procedures that are not well understood in theory and can potentially be unstable in practice. To address this difficulty, we propose a mixing strategy that leverages available arbitrary models to improve their individual performances. The proposed method is computationally efficient and almost tuning-free; thus, it can be used as an off-the-shelf method for network modeling. We show that the proposed method performs equally well as the oracle estimate when the true model is included as individual candidates. More importantly, the method remains robust and outperforms all current estimates even when the models are misspecified. Extensive simulation examples are used to verify the advantage of the proposed mixing method. Evaluation of link prediction performance on 385 real-world networks from six domains also demonstrates the universal competitiveness of the mixing method across multiple domains.
Informative core identification in complex networks
Jan 16, 2021



Abstract:In network analysis, the core structure of modeling interest is usually hidden in a larger network in which most structures are not informative. The noise and bias introduced by the non-informative component in networks can obscure the salient structure and limit many network modeling procedures' effectiveness. This paper introduces a novel core-periphery model for the non-informative periphery structure of networks without imposing a specific form for the informative core structure. We propose spectral algorithms for core identification as a data preprocessing step for general downstream network analysis tasks based on the model. The algorithm enjoys a strong theoretical guarantee of accuracy and is scalable for large networks. We evaluate the proposed method by extensive simulation studies demonstrating various advantages over many traditional core-periphery methods. The method is applied to extract the informative core structure from a citation network and give more informative results in the downstream hierarchical community detection.
Community models for partially observed networks from surveys
Aug 09, 2020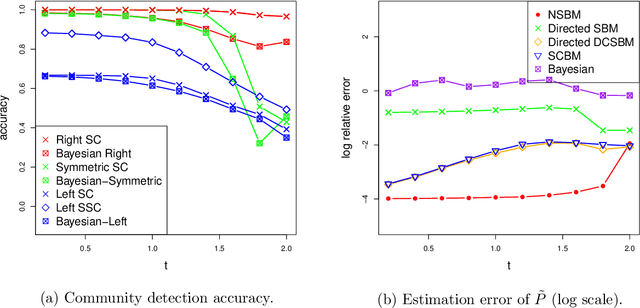
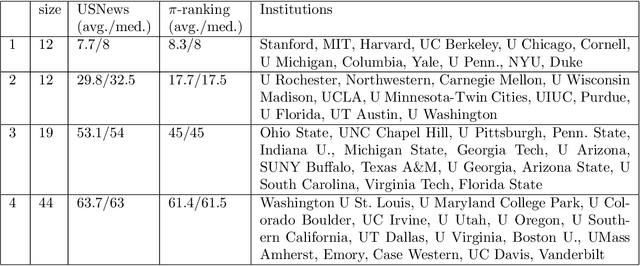
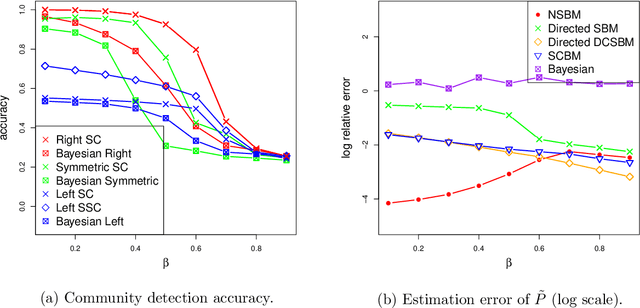
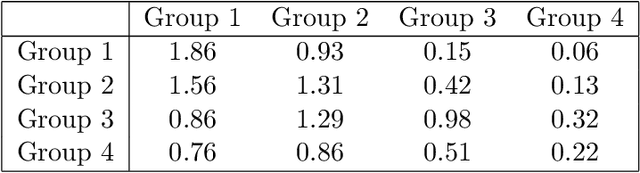
Abstract:Communities are a common and widely studied structure in networks, typically under the assumption that the network is fully and correctly observed. In practice, network data are often collected through sampling schemes such as surveys. These sampling mechanisms introduce noise and bias which can obscure the community structure and invalidate assumptions underlying standard community detection methods. We propose a general model for a class of network sampling mechanisms based on survey designs, designed to enable more accurate community detection for network data collected in this fashion. We model edge sampling probabilities as a function of both individual preferences and community parameters, and show community detection can be done by spectral clustering under this general class of models. We also propose, as a special case of the general framework, a parametric model for directed networks we call the nomination stochastic block model, which allows for meaningful parameter interpretations and can be fitted by the method of moments. Both spectral clustering and the method of moments in this case are computationally efficient and come with theoretical guarantees of consistency. We evaluate the proposed model in simulation studies on both unweighted and weighted networks and apply it to a faculty hiring dataset, discovering a meaningful hierarchy of communities among US business schools.
High-dimensional Gaussian graphical model for network-linked data
Jul 04, 2019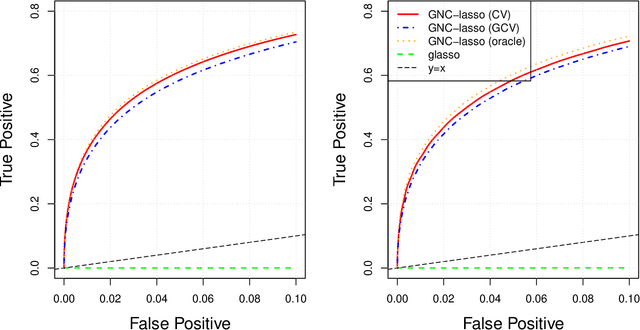
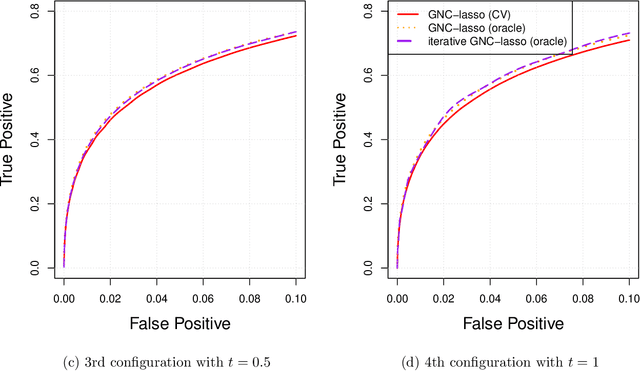
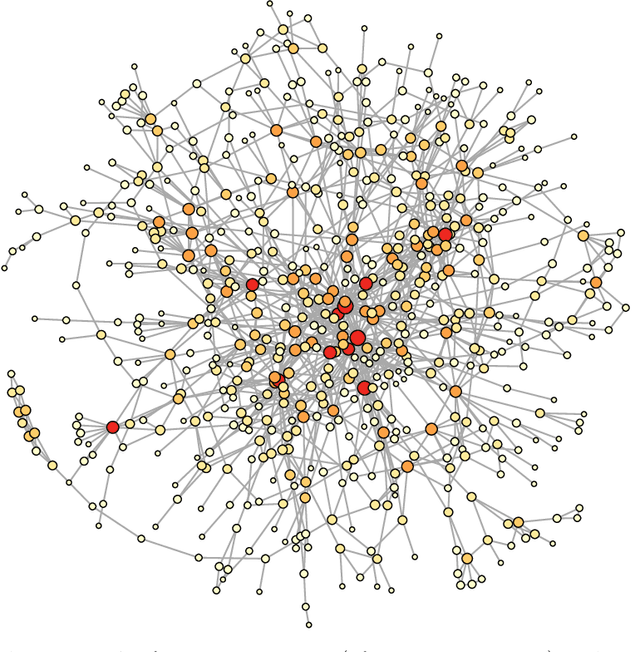
Abstract:Graphical models are commonly used to represent conditional dependence relationships between variables. There are multiple methods available for exploring them from high-dimensional data, but almost all of them rely on the assumption that the observations are independent and identically distributed. At the same time, observations connected by a network are becoming increasingly common, and tend to violate these assumptions. Here we develop a Gaussian graphical model for observations connected by a network with potentially different mean vectors, varying smoothly over the network. We propose an efficient estimation algorithm and demonstrate its effectiveness on both simulated and real data, obtaining meaningful interpretable results on a statistics coauthorship network. We also prove that our method estimates both the inverse covariance matrix and the corresponding graph structure correctly under the assumption of network "cohesion", which refers to the empirically observed phenomenon of network neighbors sharing similar traits.
Hierarchical community detection by recursive bi-partitioning
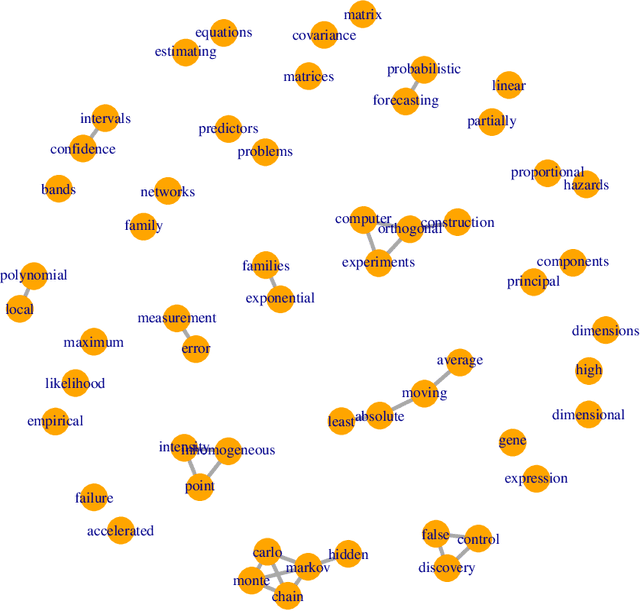
Oct 02, 2018

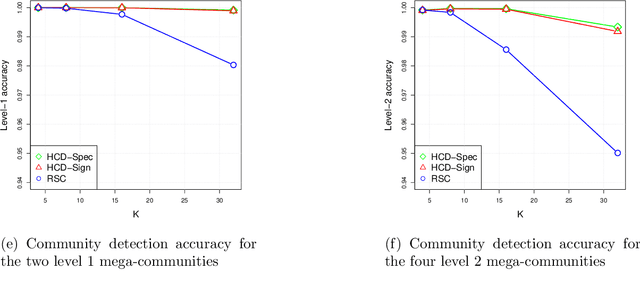

Abstract:The problem of community detection in networks is usually formulated as finding a single partition of the network into some "correct" number of communities. We argue that it is more interpretable and in some regimes more accurate to construct a hierarchical tree of communities instead. This can be done with a simple top-down recursive bi-partitioning algorithm, starting with a single community and separating the nodes into two communities by spectral clustering repeatedly, until a stopping rule suggests there are no further communities. Such an algorithm is model-free, extremely fast, and requires no tuning other than selecting a stopping rule. We show that there are regimes where it outperforms $K$-way spectral clustering, and propose a natural model for analyzing the algorithm's theoretical performance, the binary tree stochastic block model. Under this model, we prove that the algorithm correctly recovers the entire community tree under relatively mild assumptions. We also apply the algorithm to a dataset of statistics papers to construct a hierarchical tree of statistical research communities.
Network cross-validation by edge sampling
May 09, 2018



Abstract:While many statistical models and methods are now available for network analysis, resampling network data remains a challenging problem. Cross-validation is a useful general tool for model selection and parameter tuning, but is not directly applicable to networks since splitting network nodes into groups requires deleting edges and destroys some of the network structure. Here we propose a new network resampling strategy based on splitting edges rather than nodes, applicable to both cross-validation and bootstrap for a wide range of network model selection tasks. We provide a theoretical justification for our method in a general setting and examples of how our method can be used in specific network model selection and parameter tuning tasks. Numerical results on simulated networks and on a citation network of statisticians show that this cross-validation approach works well for model selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge