Community models for partially observed networks from surveys

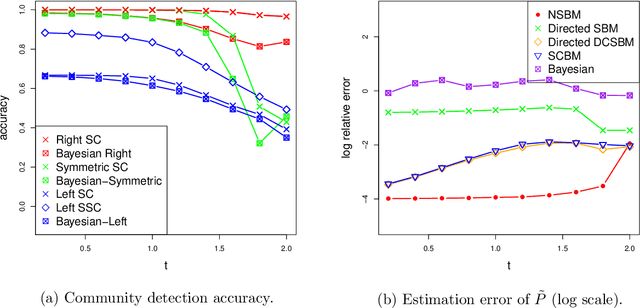
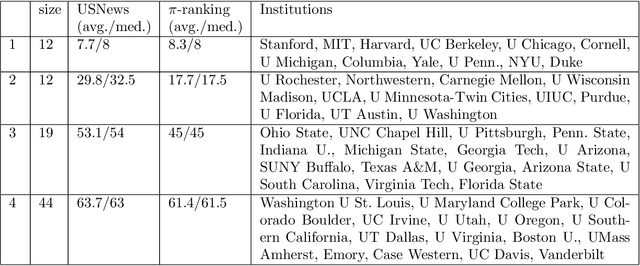
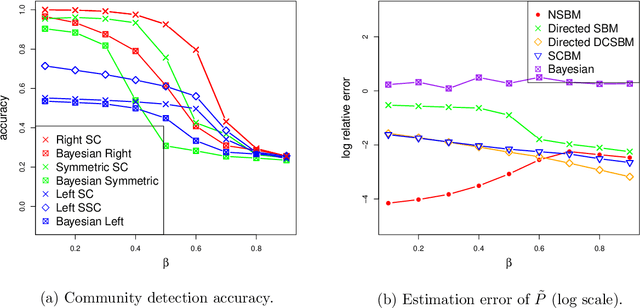
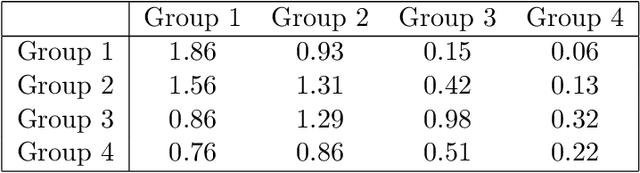
Communities are a common and widely studied structure in networks, typically under the assumption that the network is fully and correctly observed. In practice, network data are often collected through sampling schemes such as surveys. These sampling mechanisms introduce noise and bias which can obscure the community structure and invalidate assumptions underlying standard community detection methods. We propose a general model for a class of network sampling mechanisms based on survey designs, designed to enable more accurate community detection for network data collected in this fashion. We model edge sampling probabilities as a function of both individual preferences and community parameters, and show community detection can be done by spectral clustering under this general class of models. We also propose, as a special case of the general framework, a parametric model for directed networks we call the nomination stochastic block model, which allows for meaningful parameter interpretations and can be fitted by the method of moments. Both spectral clustering and the method of moments in this case are computationally efficient and come with theoretical guarantees of consistency. We evaluate the proposed model in simulation studies on both unweighted and weighted networks and apply it to a faculty hiring dataset, discovering a meaningful hierarchy of communities among US business schools.