Pseudo-likelihood methods for community detection in large sparse networks

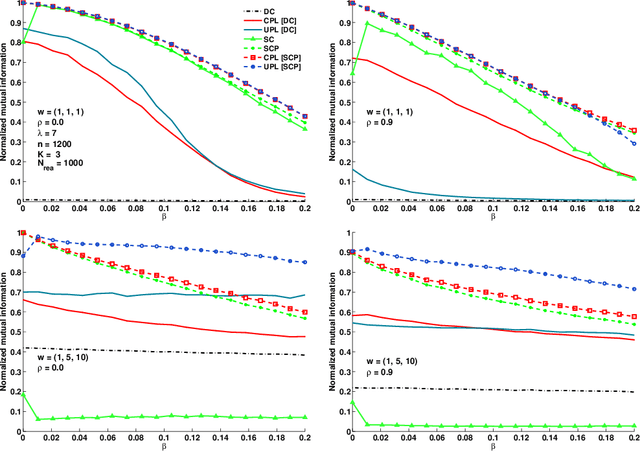
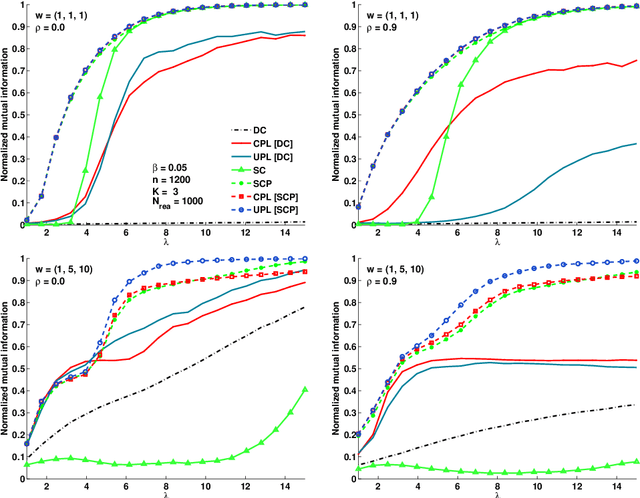
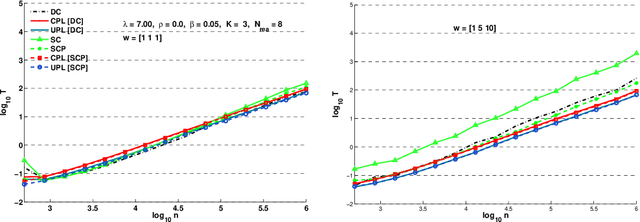
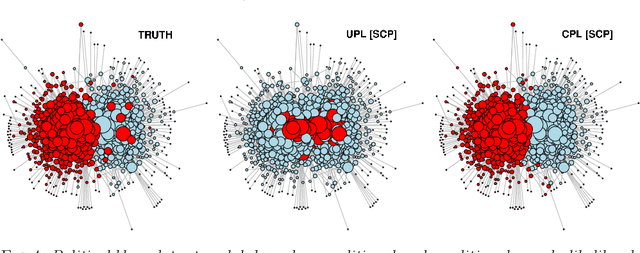
Many algorithms have been proposed for fitting network models with communities, but most of them do not scale well to large networks, and often fail on sparse networks. Here we propose a new fast pseudo-likelihood method for fitting the stochastic block model for networks, as well as a variant that allows for an arbitrary degree distribution by conditioning on degrees. We show that the algorithms perform well under a range of settings, including on very sparse networks, and illustrate on the example of a network of political blogs. We also propose spectral clustering with perturbations, a method of independent interest, which works well on sparse networks where regular spectral clustering fails, and use it to provide an initial value for pseudo-likelihood. We prove that pseudo-likelihood provides consistent estimates of the communities under a mild condition on the starting value, for the case of a block model with two communities.

Cluster Forests

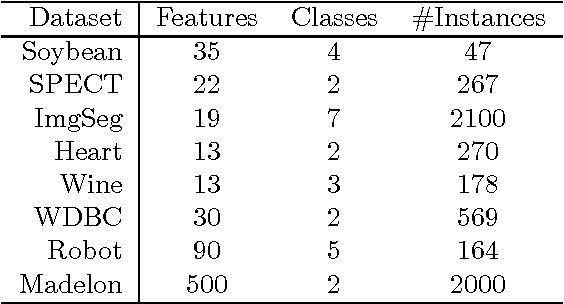
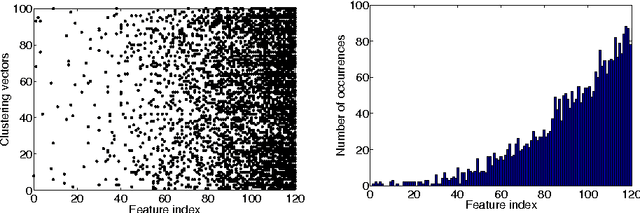
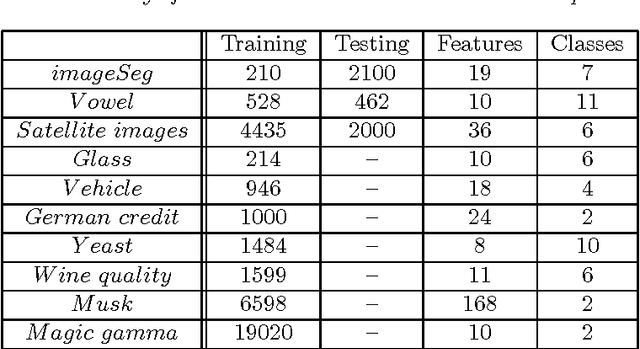
With inspiration from Random Forests (RF) in the context of classification, a new clustering ensemble method---Cluster Forests (CF) is proposed. Geometrically, CF randomly probes a high-dimensional data cloud to obtain "good local clusterings" and then aggregates via spectral clustering to obtain cluster assignments for the whole dataset. The search for good local clusterings is guided by a cluster quality measure kappa. CF progressively improves each local clustering in a fashion that resembles the tree growth in RF. Empirical studies on several real-world datasets under two different performance metrics show that CF compares favorably to its competitors. Theoretical analysis reveals that the kappa measure makes it possible to grow the local clustering in a desirable way---it is "noise-resistant". A closed-form expression is obtained for the mis-clustering rate of spectral clustering under a perturbation model, which yields new insights into some aspects of spectral clustering.

Classification under Data Contamination with Application to Remote Sensing Image Mis-registration

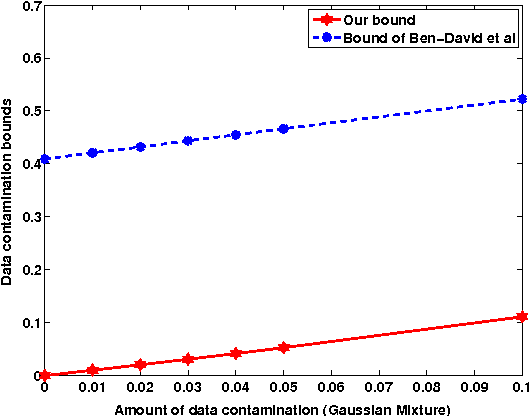
This work is motivated by the problem of image mis-registration in remote sensing and we are interested in determining the resulting loss in the accuracy of pattern classification. A statistical formulation is given where we propose to use data contamination to model and understand the phenomenon of image mis-registration. This model is widely applicable to many other types of errors as well, for example, measurement errors and gross errors etc. The impact of data contamination on classification is studied under a statistical learning theoretical framework. A closed-form asymptotic bound is established for the resulting loss in classification accuracy, which is less than $\epsilon/(1-\epsilon)$ for data contamination of an amount of $\epsilon$. Our bound is sharper than similar bounds in the domain adaptation literature and, unlike such bounds, it applies to classifiers with an infinite Vapnik-Chervonekis (VC) dimension. Extensive simulations have been conducted on both synthetic and real datasets under various types of data contamination, including label flipping, feature swapping and the replacement of feature values with data generated from a random source such as a Gaussian or Cauchy distribution. Our simulation results show that the bound we derive is fairly tight.

Efficient independent component analysis

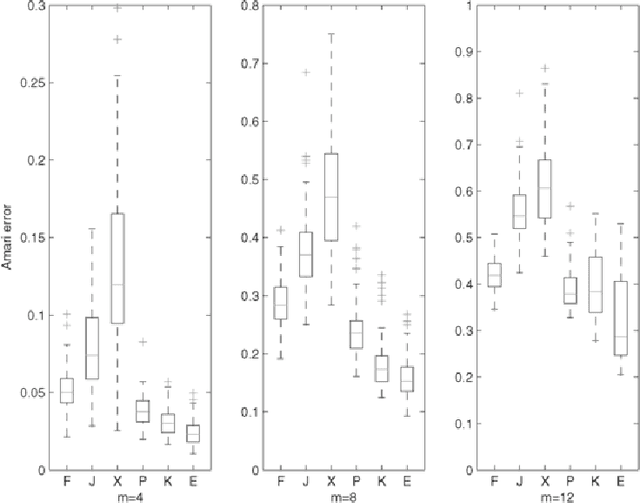
Independent component analysis (ICA) has been widely used for blind source separation in many fields such as brain imaging analysis, signal processing and telecommunication. Many statistical techniques based on M-estimates have been proposed for estimating the mixing matrix. Recently, several nonparametric methods have been developed, but in-depth analysis of asymptotic efficiency has not been available. We analyze ICA using semiparametric theories and propose a straightforward estimate based on the efficient score function by using B-spline approximations. The estimate is asymptotically efficient under moderate conditions and exhibits better performance than standard ICA methods in a variety of simulations.